
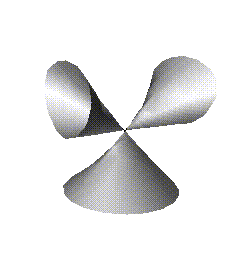

Richard Morris
(rich@singsurf.org)
University of Liverpool
July, 1992
This paper was presented at the Fifth IMA confrence on the Mathematics
of Surfaces at Edinbrugh University, 1992 and appears in
Design and Applications of Curves and Surfaces, Ed R.B. Fisher, Clarendon Press, Oxford, 1994
In this paper we describe a program for drawing algebraic surfaces in . Strictly speaking it draws the zero sets of implicit polynomials . The program produces a model of the surface which can be viewed using a general rendering package. The program has been specially designed to draw singular surfaces accurately and find all the components of the surface.
There are many programs already existing which do this to a limited extent. Programs to draw surfaces of the type z=f(x,y) have been around for a number of years. CAD systems can draw specific types of algebraic surfaces but not normally singular ones. There are a few existing programs which draw general algebraic surfaces. Ray tracers [5] can be used to produce beautiful pictures of algebraic surface but they are slow and only gives the view from one direction. Other programs such the contour tracer written by the Geometry Supercomputer Project [2], produce good results but do not pay mush attention to singularities and may give topologically incorrect results.
A hybrid method has been used in the algorithm using recursive sub-division, Bernstein polynomials and a little differential geometry. The division of the surface into cells also plays an important part in the algorithm.
Thanks must go to R. Martin who introduced me to A. Geisow's method [3] for drawing algebraic curves in the plane which is based on Bernstein polynomials, D. Marsh for useful conversations and an overview of possible techniques, C. Gibson for doubting whether it was possible and hence providing the motivation and finally all those in the Liverpool University Pure Mathematics Department who produced many practical examples to test the routine on.
The pictures produced in this paper have been produced using an implementation of the algorithm running on a Silicon Graphics Iris 4D-GT graphics workstation provided by the S.E.R.C. under a computer science initiative grant. The models were displayed using the geomview package written at the Geometry Center, University of Minnesota.


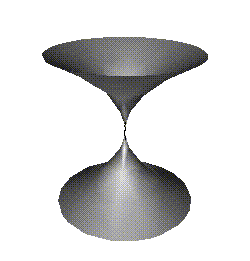
Figure 1: Two smooth surfaces showing curves along which the partial derivatives vanish


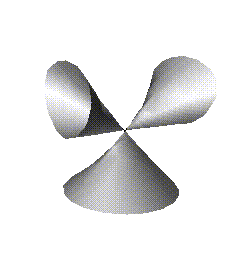

Figure 2: Zero contours of some of the standard germs


Figure 3: A cross-cap and a triple point

Figure 4: A swallowtail surface
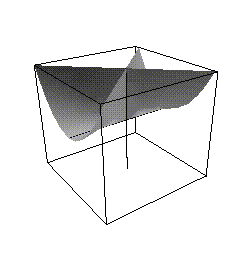
Figure 5: Dividing a cross-cap into cells
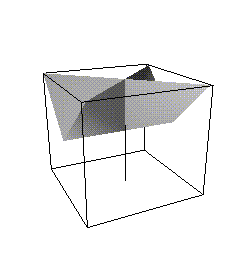
Figure 6: approximating the cross-cap of Fig. 5 by a set of facets and lines
Figure 7: Finding solutions on an edge
Figure 8: Faces where one of the partial derivatives vanishes
Figure 9: Faces where two partial derivatives vanish
Back to My Papers