A Web-based Client-Server System

for the Calculation of Algebraic Surfaces

Richard Morris

Department of Statistics, University of Leeds

A Client-Server System for the Visualisation of Algebraic Surfaces on the Web full paper (PDF).

Slides

Abstract

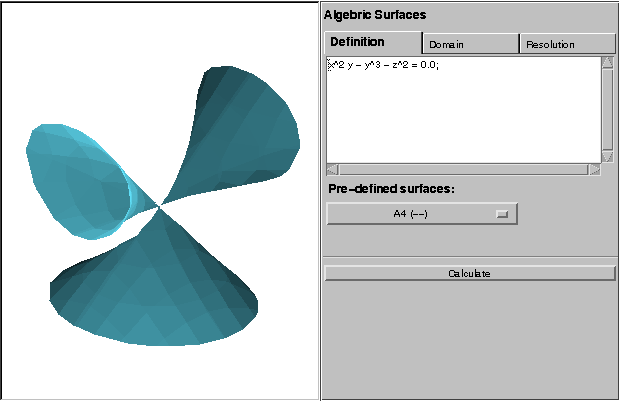
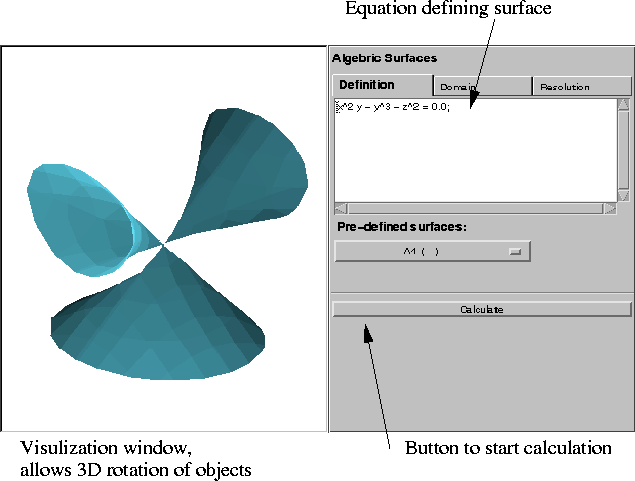
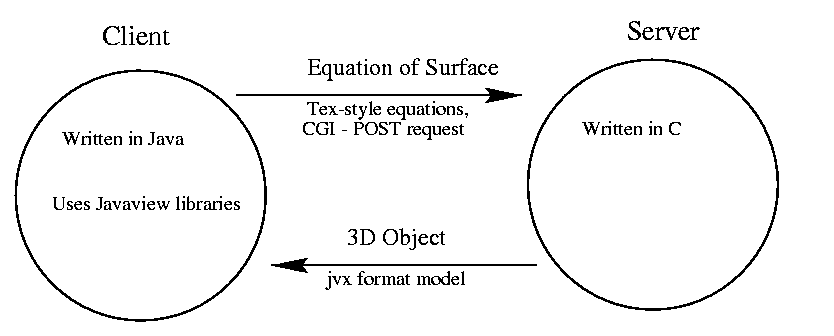
Algebraic surfaces, defined as the zero set of a polynomial function in three variables, present particular problem for visualizing, especially if the surface contains singularities. Most algorithms for constructing a polygonization of the surface will miss the singular points. We present an algorithm for polygonizing such surfaces which attempts to get accurate representations of the singular points. A client-server approach is used to enable the visualization of the polygonal mesh in a web browser. The client is a Java applet which uses the Javaview library which allows the 3D rotation and scaling of the object. The server is a C program which takes the definition of the surface and calculates the polygonization. The client connect to the server using the CGI protocol. This system allows algebraic surfaces to be viewed in any web browser on any platform.

Key Features

Calculates 3D models of Algebraic Surfaces
i.e. solutions of f(x,y,z) = 0
Special attention is paid to surfaces containing singularities
Uses Java/Javaview which allows it to run on any platform
Javaview provides interactive rotation of 3D models
Client-Server approach allows legacy code to be used and minimises download time

A Brief Tour of Algebraic Surfaces

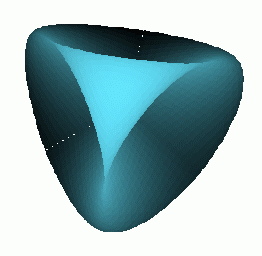
Many famous surfaces are defined as algebraic surfaces


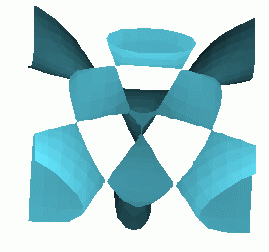
Steiner's Roman Surface	Kummer Surface	Boys Surface

The Kummer surfaces form a parametrised family of surface.

Singular Surface

Of particular interest are surfaces which contain singularities

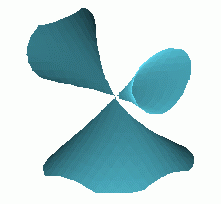
A1:
x^2 + y^2 - z^2=0 A3:
x^2 + y^2 - z^4=0 D4:
x^2 y - y^3 - z^2=0 E7:
x^3-x y^3 - z^2 =0

These provide a particular challenge for accurate rendering.

Other surfaces can be very degenerate


Cross Cap: x^2 y - z^2 = 0	triple point: x y z = 0	Swallowtail: 4 z^3 y^2 - 27 y^4 + 16 x z^4 -128 x^2 z^2 - 144 x y^2 z + 256 x^3 = 0

The swallowtail surface is the discriminate surface for the set of quartic polynomials x^4 + a x^2 + b x + c. Giving values of a,b,c where the polynomial has a repeated root.

The User Interface

Fairly sophisticated syntax allows substitutions, vector operations and symbolic differentiation.

Overview of operation

Calculation of Surface

Uses Bernstein basis to represent polynomials
Uses oct-tree recursive sub division
Easy test for possible existence of zeros allows early pruning of the search tree

Algorithm adapted from a 2D algorithm for Algebraic Curves written by A Geisow.

Bernstein Polynomials

In 1-D a polynomial B(x) of degree n can be written as

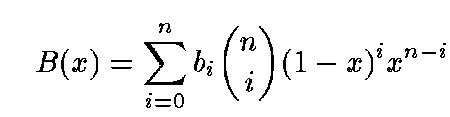
where the b_i are the Bernstein coefficients. Easy extension to 3-D.

Test for zeros

If b_i > 0 for i= 0 ... n

Then B(x) >0 for x in [0,1]

This gives a quick test to see whether a region contains a zero. The reverse does not necessarily follow.

Testing for singularities

f(x,y,z) will have a singularity at (x,y,z) if

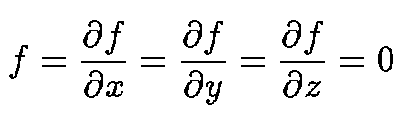
This may be an isolated point, a double cone or some more complicated singularity depending on the values of the higher derivatives.

A test on Bernstein coefficients is used to test for the possible presence of singularities

Basic operation of algorithm

Start with large box

Subdivide into 8 smaller boxes

use test for zeros to eliminate boxes which do not contain a part of the surface

repeat stages 2,3,4 until fixed depth reached

Find solutions on the edges, faces and interior of smaller box

Link singularities together to create a polygonization of the surface

Finding Solutions

In each smaller box various different types of solution are found.

Resolving Faces

Subdivide each face into four sub-faces
Find solutions on the edges of the faces
Check for simple cases where no derivatives vanish
Subdivide more complicated faces. Stop at pre-set depth
Link together all solutions found.

Problem Faces

For some situations it can be hard to resolve the faces

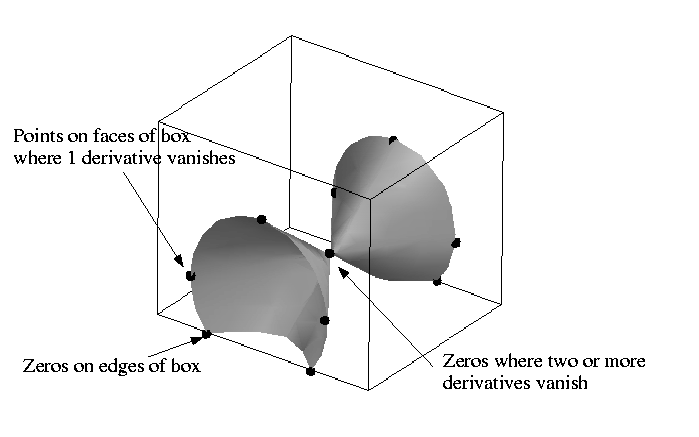
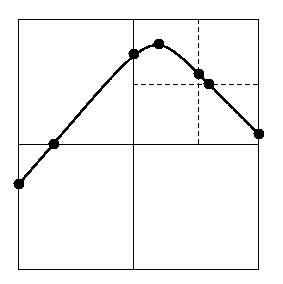
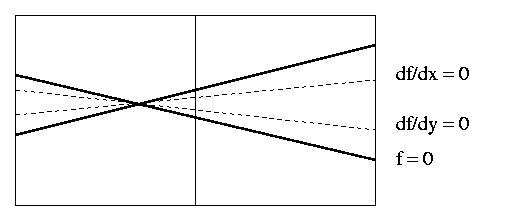
In both cases two derivatives vanish in each box.

However, only the left hand box should be marked as containing a node.

This situation cannot be resolved by finer subdivision

Finding Singularities

Used to find two different types of solution:

those where two derivatives vanish (north pole on a sphere).
real singularities where all three derivatives vanish.

Recursive subdivision of the boxes is used to find solutions where two or more derivatives vanish.

Often many false singularities found.

Constructing the skeleton

Once the solutions have been found a skeleton of the surface can be produces.

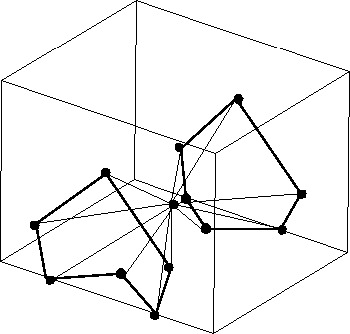
Information gathered in the previous steps used to find how solutions link together.

Constructing the polygonization

First find chains of solutions on the edges and faces of the box
Then grow the polygons inwards along the edges of the skeleton

Not 100% reliable as there can be many singularities inside a box.

History

The program was first written in 1992 and used the Geomview visualisation program.

In 1999 it was adapted to run as server producing VRML models, in a client-server system.

In 2000/2001 it was modified to produce JVX models and a user interface was constructed using the Javaview package.

Advantages of this approach

Runs on any platform.
Does not require specialist software/hardware.
3D models can give a better feel for the surface.
Allows particular regions to be examined closely.
Interactive system allows parametrised families to be examined.

Disadvantages

Initial load time can be long.
Not as visually appealing pictures as those produced by a ray tracer.
Does not produce 100% accurate models.
Java security restrictions mean that the web-page, applet and server must be on the same host.

Extensions

Non polynomial equations
Stand-alone system on a PC
Improve calculation around singular points
Add a wider range of types of curves and surface:
- Algebraic curves
- Parametrised curves/surface
- Intersections/clipping (clip existing object by a sphere or any other surface)
- apply mappings to a surface (e.g. projection)


A1: x^2 + y^2 - z^2=0	A3: x^2 + y^2 - z^4=0	D4: x^2 y - y^3 - z^2=0	E7: x^3-x y^3 - z^2 =0