Wallpaper groups are a nice way to explain some of the key concepts in group theory, and offers some non-trivial examples.
Firstly: what is a group? A group is a generalisation of addition of integers. Addition has an operator: +, that takes two elements and returns a third. It has and identity element, 0, such that for any integer, $n$, $0+n = n$ and $n+0 = 0$, and every element, $n$, has an inverse, $-n$, such that $n+(-n)=0\, (-n)+n=0$. The operation is associative meaning $a+(b+c)=(a+b)+c$. The interger with addition and also commutative so $a+b=b+c$ so forms a abelian group not all groups need to be commutative. We write the this group as $(\mathbb{Z},+)$.
A formal definition of a group, $(G,\circ)$, is a set $G$ with operator $\circ:G\times G\to G$ such that
Its sometimes useful to say the group is closed under the opertator $\circ$, this means that $g\circ h \in G$. Its not a formal part of the definition but it can be a useful check to ensure we have not missed any elements out.
If we futher have
Then the group is said to be an abelian group.
Each Wallpaper pattern is an example of a group. In each case the elements of the group will be transformations of the plane, so for each element $g \in G$ there is a transformation $T_g : \mathbb{R}^2 \to \mathbb{R}^2$. We will write
The exact set of elements depend on the type of group. Each group will have an infinite set of elements, including a two dimensional set of translations, and optionally infinite sets of rotations, reflections and glide-reflections. Before we look at these infinite groups its useful to study the finite groups that we find in the cyclic and dihedral groups.
For finite group, that has a finite number of elements, it can be useful to use a table listing the results of the group operators for each pair of elements, called the Cayley table. If a group $G$ has elements $\{I,a,b\}$ then its Cayley table is
| $\circ$ | $I$ | $a$ | $b$ |
|---|---|---|---|
| $I$ | $I\circ I$ | $I\circ a$ | $I\circ b$ |
| $a$ | $a\circ I$ | $a\circ a$ | $a\circ b$ |
| $b$ | $b\circ I$ | $b\circ a$ | $b\circ b$ |
The simplest possible group is called the trivial group which has a single element $I$. We have $I\circ I=I$ so this element is the identity element and it is its own inverse. The operation is both associative and comutative. We will denote such a group by $1$.
Next consider the cyclic groups $C_n$, consting of n-fold rotations about the origin. There is a simple rule for combining two rotations $R_\theta \circ R_\phi = R_{\theta+\phi \mod 360^\circ}$.
| $\circ$ | $I$ | $R_{180}$ |
|---|---|---|
| $I$ | $I$ | $R_{180}$ |
| $R_{180}$ | $R_{180}$ | $I$ |
| $\circ$ | $I$ | $R_{120}$ | $R_{240}$ |
|---|---|---|---|
| $I$ | $I$ | $R_{120}$ | $R_{240}$ |
| $R_{120}$ | $R_{120}$ | $R_{240}$ | I |
| $R_{240}$ | $R_{240}$ | $I$ | $R_{120}$ |
| $\circ$ | $I$ | $R_{90}$ | $R_{180}$ | $R_{270}$ |
|---|---|---|---|---|
| $I$ | $I$ | $R_{90}$ | $R_{180}$ | $R_{270}$ |
| $R_{90}$ | $R_{90}$ | $R_{180}$ | $R_{270}$ | $I$ |
| $R_{180}$ | $R_{180}$ | $R_{270}$ | $I$ | $R_{90}$ |
| $R_{270}$ | $R_{270}$ | $I$ | $R_{90}$ | $R_{180}$ |
| $\circ$ | $I$ | $R_{72}$ | $R_{144}$ | $R_{216}$ | $R_{288}$ |
|---|---|---|---|---|---|
| $I$ | $I$ | $R_{72}$ | $R_{144}$ | $R_{216}$ | $R_{288}$ |
| $R_{72}$ | $R_{72}$ | $R_{144}$ | $R_{216}$ | $R_{288}$ | $I$ |
| $R_{144}$ | $R_{144}$ | $R_{216}$ | $R_{288}$ | $I$ | $R_{72}$ |
| $R_{216}$ | $R_{216}$ | $R_{288}$ | $I$ | $R_{72}$ | $R_{144}$ |
| $R_{288}$ | $R_{288}$ | $I$ | $R_{72}$ | $R_{144}$ | $R_{216}$ |
| $\circ$ | $I$ | $R_{60}$ | $R_{120}$ | $R_{180}$ | $R_{240}$ | $R_{300}$ |
|---|---|---|---|---|---|---|
| $I$ | $I$ | $R_{60}$ | $R_{120}$ | $R_{180}$ | $R_{240}$ | $R_{300}$ |
| $R_{60}$ | $R_{60}$ | $R_{120}$ | $R_{180}$ | $R_{240}$ | $R_{300}$ | $I$ |
| $R_{120}$ | $R_{120}$ | $R_{180}$ | $R_{240}$ | $R_{300}$ | $I$ | $R_{60}$ |
| $R_{180}$ | $R_{180}$ | $R_{240}$ | $R_{300}$ | $I$ | $R_{60}$ | $R_{120}$ |
| $R_{240}$ | $R_{240}$ | $R_{300}$ | $I$ | $R_{60}$ | $R_{120}$ | $R_{180}$ |
| $R_{300}$ | $R_{300}$ | $I$ | $R_{60}$ | $R_{120}$ | $R_{180}$ | $R_{240}$ |
All these groups is closed, and commutative.
Theres groups also have the property that they are generated by a single element. Write $g^2 = g \circ g$, $g^3 = g \circ g \circ g$, etc. If every element of a group has the form $g^n$ for some integer $n$ then the group is said to be generated by $g$.
As the identity is an element of the group then $I = g^N$ for some integer $N$, and we say $g$ has order $N$. If all elements of a group has order $N$ or less, the group is said to have order $N$.
For the cyclic groups: $C_2$ is generated by $R_{180}$ and has order 2, $C_3$ is generated by $R_{120}$ and has order 3, $C_4$ is generated by $R_{90}$ and has order 4, $C_5$ is generated by $R_{72}$ and has order 5, $C_6$ is generated by $R_{60}$ and has order 6. Other elements can also generate the group, for $C_2$, $C_3$ and $C_5$ every element apart from the identity is a generator for the group. For $C_4$, $R_{90}$ and $R_{270}$ are generators, but $R_{180}$ is not. The element only has order 2. For $C_6$ $R_{60}$ and $R_{300}$ are generators of order 6, but $R_{120}$ and $R_{240}$ have order 3, and $R_{180}$ has order 2. You may notice a connection with prime numbers and factorisation here.
Now consider the group $D_n$ of dihedral rotations, which is the group of symmetries of a regular polygon with $n$ sides. Each of these has at least one reflection.
| $\circ$ | $I$ | $M_{0}$ |
|---|---|---|
| $I$ | $I$ | $M_{0}$ |
| $M_{0}$ | $M_{0}$ | $I$ |
| $\circ$ | $I$ | $R_{180}$ | $M_{0}$ | $M_{90}$ |
|---|---|---|---|---|
| $I$ | $I$ | $R_{180}$ | $M_{0}$ | $M_{90}$ |
| $R_{180}$ | $R_{180}$ | $I$ | $M_{90}$ | $M_{0}$ |
| $M_{0}$ | $M_{0}$ | $M_{90}$ | $I$ | $R_{180}$ |
| $M_{90}$ | $M_{90}$ | $M_{0}$ | $R_{180}$ | $I$ |
| $\circ$ | $I$ | $R_{120}$ | $R_{240}$ | $M_{0}$ | $M_{60}$ | $M_{120}$ |
|---|---|---|---|---|---|---|
| $I$ | $I$ | $R_{120}$ | $R_{240}$ | $M_{0}$ | $M_{60}$ | $M_{120}$ |
| $R_{120}$ | $R_{120}$ | $R_{240}$ | $I$ | $M_{60}$ | $M_{120}$ | $M_{0}$ |
| $R_{240}$ | $R_{240}$ | $I$ | $R_{120}$ | $M_{120}$ | $M_{0}$ | $M_{60}$ |
| $M_{0}$ | $M_{0}$ | $M_{120}$ | $M_{60}$ | $I$ | $R_{240}$ | $R_{120}$ |
| $M_{60}$ | $M_{60}$ | $M_{0}$ | $M_{120}$ | $R_{120}$ | $I$ | $R_{240}$ |
| $M_{120}$ | $M_{120}$ | $M_{60}$ | $M_{0}$ | $R_{240}$ | $R_{120}$ | $I$ |
| $\circ$ | $I$ | $R_{90}$ | $R_{180}$ | $R_{270}$ | $M_{0}$ | $M_{45}$ | $M_{90}$ | $M_{135}$ |
|---|---|---|---|---|---|---|---|---|
| $I$ | $I$ | $R_{90}$ | $R_{180}$ | $R_{270}$ | $M_{0}$ | $M_{45}$ | $M_{90}$ | $M_{135}$ |
| $R_{90}$ | $R_{90}$ | $R_{180}$ | $R_{270}$ | $I$ | $M_{45}$ | $M_{90}$ | $M_{135}$ | $M_{0}$ |
| $R_{180}$ | $R_{180}$ | $R_{270}$ | $I$ | $R_{90}$ | $M_{90}$ | $M_{135}$ | $M_{0}$ | $M_{45}$ |
| $R_{270}$ | $R_{270}$ | $I$ | $R_{90}$ | $R_{180}$ | $M_{135}$ | $M_{0}$ | $M_{45}$ | $M_{90}$ |
| $M_{0}$ | $M_{0}$ | $M_{135}$ | $M_{90}$ | $M_{45}$ | $I$ | $R_{270}$ | $R_{180}$ | $R_{90}$ |
| $M_{45}$ | $M_{45}$ | $M_{0}$ | $M_{135}$ | $M_{90}$ | $R_{90}$ | $I$ | $R_{270}$ | $R_{180}$ |
| $M_{90}$ | $M_{90}$ | $M_{45}$ | $M_{0}$ | $M_{135}$ | $R_{180}$ | $R_{90}$ | $I$ | $R_{270}$ |
| $M_{135}$ | $M_{135}$ | $M_{90}$ | $M_{45}$ | $M_{0}$ | $R_{270}$ | $R_{180}$ | $R_{90}$ | $I$ |
$D_3$ is our first example of a non-commuative group, where there are some elements $a,b\in D_3$ for which $a\circ b\ne b\circ a$. Here $R_{90}\circ M_0 = M_{45}$ but $M_0\circ R_{90}=M_{135}$. In other words a reflection in the x-axis follow by a 90º rotation is different to 90º rotation followed by a reflection in the x-axis. The order in which we apply tranfomations matter.
You may notice some of these group share some elements of other groups, and we can discuss the idea of sub-groups. A group $(H,\circ)$ is a subgroup of a larger group $(G,\circ)$ if the elements of $H$ is a subset of the elements of $G$ and $H$ is a group closed under the group operation $\circ$. As $H$ is a group it must contain the identity element and the inverse of every element of $H$ must lie in $H$. We write $H \le G$, and if $H$ is not identical to $G$ then $H$ is a propper subgroup and we write $H < G$.
We have several subgroups relations in our set above:
Alternative we can list the subgroups of our groups, (omitting the tivial group and the group itself)
So even with this small list of groups we have a rich structure.
It is useful to determine when two group are the same. First we need to discuss maps between groups. If $(G,*)$, $(H,\circ)$ are two groups we can consider a map between the sets $f : G \to H$ given by $g \to f(g)$. Usual we want the map to be consistant with the group operators, so if $a,b \in G$ then $$f(a)\circ f(b)=f(a * b)$$ This implies that if $I_G$ and $I_H$ are the two identity elements then the map send one to the other $f(I_G)=I_H$, and also that is consistant with inverse elements $f(a^{-1}) = (f(a))^{-1}$. Such maps are called Group homomorphisms.
We can further classify such maps according whether they are 1-to-1, or onto.
And define two important sets
$ker(f)$ is a subgroup of $G$ and $img(f)$ is a subgroup of $H$. If $f$ is a monomorphism then $ker(f)=I_G$ and if $f$ is an epimorphism then $img(f)=H$. So for isomorphisms $ker(f)=I_G$ and $img(f)=H$.
There are a few standard homoemorphisms
We can look at our current list of groups to see if they are isomorphic. We only need to consider the groups with the same number of elements.
An exact sequence is a diagram showing a sequences of groups and homomorphism between them $$A \xrightarrow{f} B \xrightarrow{g} C,$$ such that $img(f) = ker(g)$. In particular we are have short exact sequence $$1 \xrightarrow{\mathrm{id}} A \xrightarrow{f} B \xrightarrow{g} C \xrightarrow{\pi_1} 1$$ with
There are several ways to combine groups to form new groups. We will discuss two of them here, the direct product and the semidirect product.
Every element in $C_6$ can be written in the form $R_{180}^m \circ R_{120}^n$ with $m\in \{0,1\}, n\in \{0,1,2\}$. So we can form a new group $C_2 \times C_3$ which has elements given by all posible pairs $(a,b)$ with $a\in C_2, b\in C_3$. and a group operation given by $(a_1,b_1) \circ (a_2,b_2) \to (a_1 \circ a_2, b_1 \circ b_2)$, here we have used the same symbol for the operator of all three groups. This group is called the direct product of the two groups.
Here the six elements of the group $C_2\times C_3$ are $\{(I,I), (R_{180},R_{240}), (I,R_{120}), (R_{180},I), (I,R_{240}), (R_{180},R_{120})\}$. And the Cayley table is
| $\circ$ | $(I,I)$ | $(R_{180},R_{240})$ | $(I,R_{120})$ | $(R_{180},I)$ | $(I,R_{240})$ | $(R_{180},R_{120})$ |
|---|---|---|---|---|---|---|
| $(I,I)$ | $(I,I)$ | $(R_{180},R_{240})$ | $(I,R_{120})$ | $(R_{180},I)$ | $(I,R_{240})$ | $(R_{180},R_{120})$ |
| $(R_{180},R_{240})$ | $(R_{180},R_{240})$ | $(I,R_{120})$ | $(R_{180},I)$ | $(I,R_{240})$ | $(R_{180},R_{120})$ | $(I,I)$ |
| $(I,R_{120})$ | $(I,R_{120})$ | $(R_{180},I)$ | $(I,R_{240})$ | $(R_{180},R_{120})$ | $(I,I)$ | $(R_{180},R_{240})$ |
| $(R_{180},I)$ | $(R_{180},I)$ | $(I,R_{240})$ | $(R_{180},R_{120})$ | $(I,I)$ | $(R_{180},R_{240})$ | $(I,R_{120})$ |
| $(I,R_{240})$ | $(I,R_{240})$ | $(R_{180},R_{120})$ | $(I,I)$ | $(R_{180},R_{240})$ | $(I,R_{120})$ | $(R_{180},I)$ |
| $(R_{180},R_{120})$ | $(R_{180},R_{120})$ | $(I,I)$ | $(R_{180},R_{240})$ | $(I,R_{120})$ | $(R_{180},I)$ | $(I,R_{240})$ |
Note how this has the same structure as $C_6$ Cayley table with the same element along the diagonals. We can create an map, $f:C_2\times C_3$ defined by $f:(I,I)\to I$, $f:(R_{180},R_{240})\to R_{60}$, $f:(I,R_{120})\to R_{120}$, $f:(R_{180},I)\ to R_{180}$, $f:(I,R_{240})\to R_{240}$, and $f:(R_{180},R_{120})\to R_{300}$. Then check it is injective, surjective and a group homomorphism.
In a similar fashion $D_4 \cong D_1 \times C_2$. The elements of $D_4$ are $\{ (I,I), (M_0,I), (I,R_{180}), (M_0,R_{180}) \}$ with
| $\circ$ | $(I,I)$ | $(M_{0},I)$ | $(I,R_{180})$ | $(M_0,R_{180})$ |
|---|---|---|---|---|
| $(I,I)$ | $(I,I)$ | $(M_0,I)$ | $(I,R_{180})$ | $(M_0,R_{180})$ |
| $(M_0,I)$ | $(M_0,I)$ | $(I,I)$ | $(M_0,R_{180})$ | $(I,R_{180})$ |
| $(I,R_{180})$ | $(I,R_{180})$ | $(M_0,R_{180})$ | $(I,I)$ | $(M_0,I)$ |
| $(M_0,R_{180})$ | $(M_0,R_{180})$ | $(I,R_{180})$ | $(M_0,I)$ | $(I,I)$ |
If $N$ and $H$ are sub groups a group $G$, we can form a new group, $N H$, consists of all elements of the form $n \circ h$ where $n\in N$ and $h\in H$. $N H = \{ n \circ h | n\in N, h\in H \}$. If $N H \cong G$ and $N \cap H = I_G$ then we say that $G$ is the internal direct product of the two subgroups $N$ and $H$ written $N\rtimes H$.
For example, the group $D_3$ is the internal direct product of the cyclic group $C_3$ and the cyclic group $D_1$. These groups have elements $\{I, R_{120}, R_{240}\}$ and $\{I, M_0\}$ respectively. The elements of this product are $\{I\circ I, R_{120}\circ I, R_{240}\circ I , I\circ M_0, R_{120} \circ M_0, R_{240} \circ M_0\}$. =$\{I, R_{120}, R_{240}, M_0, M_{240}, M_{120}\}$.
Even though $C_3\times C_2$ and $C_3 \rtimes C_2$ have the same number of elements they have different group structure. Consider pairs of elements $a_1,a_2 \in C_3$, $b_1,b_2 \in C_2$ Then in $C_3\times C_2$ we have two elements $(a_1,b_1)$ and $(a_2,b_2)$ and there product is $(a_1\circ a_2,b_1\circ b_2)$, under the isomorphism $f(a,b) = a\circ b$ this product becomes $(a_1\circ a_2)\circ(b_1\circ b_2)$. In $C_3\rtimes C_2$ the two elements are $a_1\circ b_1$ and $a_2\circ b_2$ and their product is $(a_1\circ b_1) \circ (a_2\circ b_2)$, the elements are multiplied in a different order.
If $N$ is a subgroup of $G$, and $g\in G$ then we can form the the left coset $aN =\{ a h : h\in N\}$ and right coset $Na = \{h a : h \in N\}$. If the left and right cosets agree $aN = Na$ for all $a\in G$ then $N$ is a normal subgroup.
For example consider $C_3 = \{I, R_{120}, R_{240}\}$ as a subgroup of $D_3$. For each element $g$ of we can form the left cosets.
Note how the first three sets are the same set, and the last three are the same set. So here we split $G$ into two disjoint sets $A = \{I, R_{120}, R_{240}\}, B = \{M_0, M_{120}, M_{60}\}$. We can form a group $Q = ( \{A, B\}, *)$ where the group operation extends naturally. This group is called the Quotient group and is normally written $G / N$. It can be thought of as factoring out the elements of $G$ by the elements of $N$.
For a general quotient group we have an exact sequence $$1 \to N \xrightarrow{\mathbf{id}} G \xrightarrow{/N} G / N \to 1$$
The quotient group $D_3 / C_3 \cong C_2$ so we have the exact sequence $$1\to C_3 \xrightarrow{\mathbf{id}} D_3 \xrightarrow{/C_3} C_2 \to 1.$$ Meaning that $img(\mathbf{id}) \in ker(/C_3)$ so every element of $C_3$ maps to the identity element.
We now have all the tools we need to understand the wallpaper groups.
For each of the 17 wallpaper patterns we define the group $W$ consisting of a set of transformations that preserve the pattern, with the composition of transformations, $\circ$ as the group operation. This group consist of a set of translations plus other translations. For example $p2$ consists of translations preserving a lattice plus one 180º around each lattice point. The group can have complicate structures which we can examine interms of subgroup and quotient groups.
Each symmetry group preserves a lattice of points, and the group of translations that preserve than lattice forms an infinite group. Part of the clasification of wallpaper groups depend on the structure of this lattice.
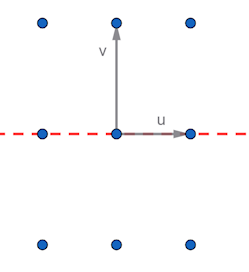
Give two linearly independent vectors $\mathbf{u}$, $\mathbf{v}$ we can define a lattice of points $\{\mathrm{O} + l\,\mathbf{u} + m\,\mathbf{v} : l, m \in \mathbb{Z}\}$ and a set of translations that preserve this latice. Let $T_{lm}$ be the translation along vector $l \mathbf{u}+ m \mathbf{v}$. We can form a translation group $$T =(\{ T_{lm} : l, m \in \mathbb{Z}\} , \circ).$$
This is our first infinite group, its abelian and the group operator is closed as combining two translations gives another translation, hence it forms a sub group of the full wallpaper group $W$. It is a normal subgroup as is invariant under conjugation by elements of $W$ i.e. if $t\in T$ and $g\in W$ then $g\,t\,g^{-1} \in T$ or equiviently $g^{-1}\,t\,g \in T$. In other words take a transformation $g$ in $W$, apply a translation, then apply the inverse of $g$, the resulting transformation is another translations. Informally
In general the resulting translation is not the initial translation.
As $T$ is a normal subgroup of the wallpaper group $W$ we can form the quotient group $W/T$ by factoring out the translation component. Giving the exact sequence $$1 \to T \to W \to W/T \to 1$$ As we factor out translations the quotient group will be a point groups that fixes a single point, either a cyclic group or dihedral group.
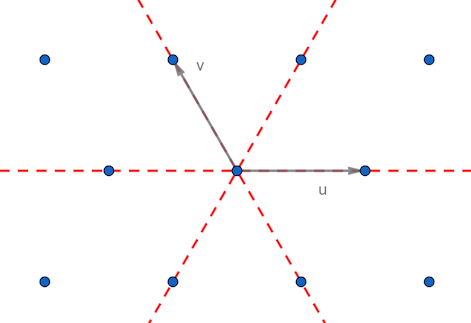
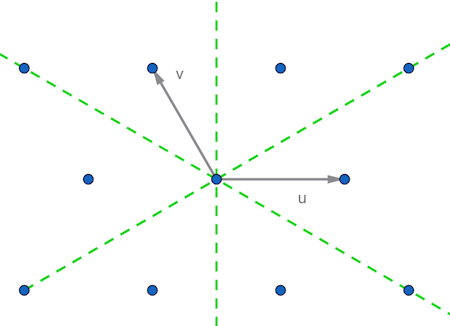
By observing which point groups preserve a lattice of points we know that the only possible point groups are $C_1, C_2, C_3, C_4, C_6, D_1, D_2, D_3, D_4, D_6$. Furthermore some wallpaper groups place restrictions on the type of lattice rhombic, rectanglar, square or rectangular lattices. So we can clasify wallpaper groups by point group and type of lattice.
Note how there are three different wallpaper groups with the same $D_1$ point group four with the same $D_2$ point group, two with the $D_3$ point group and two with $D_4$ point group. We can distinguish between some of these by considering how the reflection in the point group aligns with the basis for the lattice. If the lines of reflection are parallel to the lattice basis vectors (short axis) or to the diagonals (long axis).

|

|

|

|
| Short axis for rectanglar lattice, PM, PG, PMM, PMG, PGG | Long axis for rhombic lattice, CM, CMM | Short axis for hexagonal lattice, P31M | Long axis for hexagonal lattice, P3M1 |
So we have two varients $D_{n,l}$, $D_{n,s}$ for each of the groups $D_1$, $D_2$ and $D_3$ giving us a total of 13 different point groups: $C_1, C_2, C_3, C_4, C_6, D_{1,l}, D_{1,s}, D_{2,l}, D_{2,s}, D_{3,l}, D_{3,s}, D_4, D_6$.
| Wallpaper group | Point group | lattice | axis |
|---|---|---|---|
| P1 | $C_1 = id$ | parallogram | |
| P2 | $C_2$ | parallogram | |
| CM | $D_{1,l}$ | rhombic | long |
| PM | $D_{1,s}$ | rectangular | short |
| PG | $D_{1,s}$ | rectangular | short |
| CMM | $D_{2,l}$ | rhombic | long |
| PMM | $D_{2,s}$ | rectangular | short |
| PMG | $D_{2,s}$ | rectangular | short |
| PGG | $D_{2,s}$ | rectangular | short |
| P4 | $C_4$ | square | |
| P4M | $D_4$ | square | |
| P4G | $D_4$ | square | |
| P3 | $C_3$ | hexagonal | |
| P3M1 | $D_{3,l}$ | hexagonal | long |
| P31M | $D_{3,s}$ | hexagonal | short |
| P6 | $C_6$ | hexagonal | |
| P6M | $D_6$ | hexagonal |
Factoring out translations, removes the distinction between reflections and glide reflections. So we need some futher tools, to distinguish between PM and PG, and between PMM, PMG and PMG. Here we can use group actions and cohomology to fully classify the Wallpaper groups and explain why there are exactly 17 such groups. Morandi has a detailed explination of this classification.
Given two groups $T$ and $Q$ we can consider the exact sequence $$1\to T\xrightarrow{i} G \xrightarrow{\pi} Q \to 1$$ and try to find the all the groups groups $G$ than give an exact sequence. $G$ is said to be an extension of $Q$ by $T$. As the sequence is exact we know that $i(T)$ is a normal sub-group of $G$ and the quotient group $G/N$ is isomorphic to $Q$. All finite groups may be constructed as a series of extensions with finite simple groups.
One way to find a group extension is to use the direct product with elements $\{(t,q) : t\in T, q\in Q\}$ and group homomorphism $i(t)=(t,1)$ and $\pi(t,q)=q$, we see $img(i)=ker(\pi)$ so we have an exact sequence. This is called the trivial extension.
Another group extension is the semi-direct product $T\rtimes Q$. Here elements of $G$ are given by $\{t\circ q : t\in T, q\in Q\}$ the group homomorphism $i(t)=t\circ 1$ and $\pi$ is the quotient map. Such extensions are called split extensions. Another property of the semi-direct product is there is a homomorphism $\gamma: Q \to G$ such that $\pi \circ \gamma: Q \to Q$ is the identity map.
For each of our 13 point groups there is a split extension, giving 13 different wallpaper groups.
The wallpaper groups PG, PMG, PGG be described as group extension but they are not split-extensions. For PG the point group is $D_{1,s}$ containing a reflection $M_0$ but the wallpaper group does not contain this reflection, so $D_1$ is not a subgroup of PG required for a split extension. Furthermore we cannot construct a homomorphism $\gamma: Q \to G$ such that $\pi \circ \gamma = id$. We could construct a map with $\gamma(I)=I$ and $\gamma(M_0)=G_\mathbf{u}$, but this fails to be a homomorphism as $$\gamma(M_0 \circ M_0) = \gamma(I) = I$$ but $$\gamma(M_0) \circ \gamma(M_0) = G_\mathbf{u} \circ G_\mathbf{u} = T_{2\mathbf{u}} \ne I$$ so it fails the condition $\gamma(a\circ b)=\gamma(a)\circ\gamma(b)$ needed for group homomorphism.
The number of possible group extensions for a given point group, $G_0$ and lattice group $T$, is given by the size of the second co-homology group $H^2(G_0,T)$. For $C_1, C_2, C_3, C_4, C_6, D_{1,l}, D_{2,l}, D_{3,l}, D_{3,s}, D_6$ we have $|H^2(G_0,T)|=1$ and a single group extension. For $D_{1,s}, D_4$ $|H^2(G_0,T)|=2$ with two group extensions. For $D_{2,s}$ the cohomology group has size four but two of the extensions give isomorphic wallpaper groups.
| Point group | |H^2(G_0,T)| | Group extensions | split |
|---|---|---|---|
| $C_1 = id$ | 1 | $1\to T\to \text{P1} \to C_1 \to 1$ | y |
| $D_{1,l}$ | 1 | $1\to T\to \text{CM} \to D_{1,l} \to 1$ | y |
| $D_{1,s}$ | 2 | $1\to T\to \text{PM} \to D_{1,s} \to 1$ | y |
| $1\to T\to \text{PG} \to D_{1,s} \to 1$ | n | ||
| $C_2$ | 1 | $1\to T\to \text{P2} \to C_2 \to 1$ | y |
| $D_{2,l}$ | 1 | $1\to T\to \text{CMM} \to D_{2,l} \to 1$ | y |
| $D_{2,s}$ | 4 | $1\to T\to \text{PMM} \to D_{2,s} \to 1$ | y |
| $1\to T\to \text{PMG} \to D_{2,s} \to 1$ | n | ||
| $1\to T\to \text{PGG} \to D_{2,s} \to 1$ | n | ||
| $C_3$ | 1 | $1\to T\to \text{P3} \to C_3 \to 1$ | y |
| $D_{3,l}$ | 1 | $1\to T\to \text{P31M} \to D_{3,l} \to 1$ | y |
| $D_{3,s}$ | 1 | $1\to T\to \text{P3M1} \to D_{3,s} \to 1$ | y |
| $D_{4,l}$ | 1 | $1\to T\to \text{P4} \to D_{4,l} \to 1$ | y |
| $D_{4,s}$ | 2 | $1\to T\to \text{P4M} \to D_{4,s} \to 1$ | y |
| $1\to T\to \text{P4G} \to D_{4,s} \to 1$ | n | ||
| $C_6$ | 1 | $1\to T\to \text{P6} \to C_6 \to 1$ | y |
| $D_6$ | 1 | $1\to T\to \text{P6M} \to D_6 \to 1$ | y |
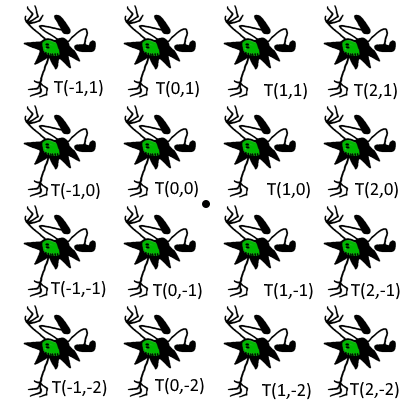
With the exact sequence $1\to T\to G\to C_4\to 1$ for each element of $x$ in $C_4$ we can define an action $A_x: T\to T$. Let $g_x \in G$ be an element in $G$ such that $\pi_{C_4}(g_x)=x$. This defines a conjugation on elements $g \in G$: $g \to g_x \circ g \circ g_x^{-1}$ and as $T$ is a normal subgroup a conjugation on elements $t \in T$: $A_x(t) = id_T^{-1} (g_x \circ id_T(t) \circ g_x^{-1})$. This is an automorphism as it preserves the identity, is both one-to-one and onto, and respects the group action.

| 
| 
|
| Applying the $g_x^{-1}$ to a motif where $x=R_{270}$ | Applying $t \circ g_x^{-1}$ for various values of $t$ | Applying $g_x \circ t \circ g_x^{-1}$ for various values of $t$ |
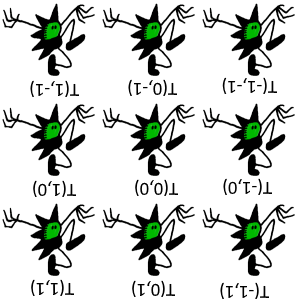
Similar actions can be constructed for the other elements of $C_4$. Each gives a different automorphism on the group $T$.
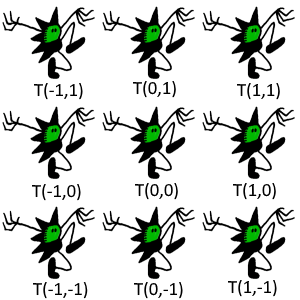
| 
| 
|
| Applying the action $I$ to $T$ | Applying the $R_{180}$ to $T$ | Applying the $R_{270}$ to $T$ |
Copyright R Morris 2025