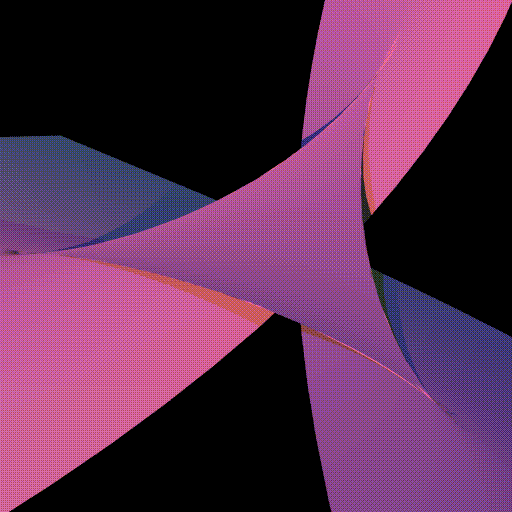
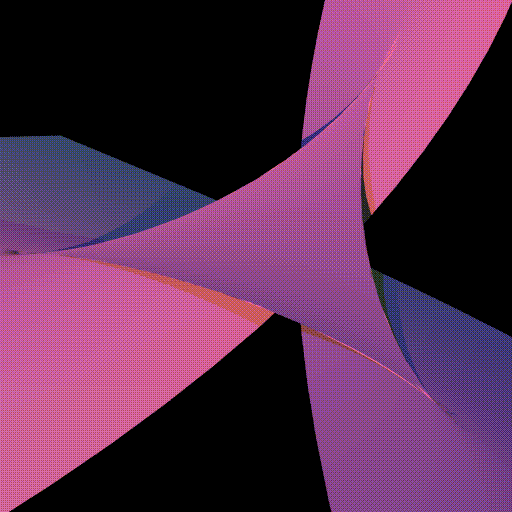
Visulising duals of surfaces (preprint)
See also
The technique used in the preprint can also be used to help visulise algebraic varities defined in $\mathbb{P}^3$ as shown in the Projective Varieties for an online visuliser.
The classification of cubics define the surfaces in three dimensional cubic space. For example a cubic with 4 double pints is defined by homogenous polynomial $x y z + x y w + x z w + y z w=0$. As this is a homogeneous polynomial if $(x,y,z,w)$ is a solution then so is $(a x, a y,a z,a w)$. This surface has four double point at $(0,0,0,1)$, $(1,0,0,0)$, $(0,1,0,0)$, and $(0,0,1,0)$ which easily shown as all derivative vanish if any three of the variables are zero. Part of the surface can be generated by fixing a plane at infinity, say $w=1$, and take the projection $(x,y,z,w)\to(x/w,y/w,z/w)$. In effect this calculates the intersection of the surface with the plane $w=1$. This results in the 3D equation $x y z + x y + x z + y z=0$ which has a single double point the other nodes lie at infinity.

One way all four nodes can be sean is to choose a different plane at infinity, for instance $x+y+z+w=0$, choosing a rotation $R:(x,y,z,w)\to(X,Y,Z,W)$ which maps this plane onto $W=\text{constant}$, and calculate the surface $f(X,Y,Z)=0$, in this case the equation $4+8 X Y Z-4*X^2-4*Y^2-4*Z^2$. This is the aproach taken on the cubic page.
Here we use a more general method. Four planes are taken $x=1$, $y=1$, $z=1$ and $w=1$ and the intesection of the surface with each planes calculated. So four 3D surfaces are calculated $y z + y w + z w + y z w=0$, $x z + x w + x z w + z w=0$, $x y + x y w + x w + y w=0$ and $x y z + x y + x z + y z=0$. For each surface we only need to calculate the surface with each variable in the range $[-1,1]$, there four planes are suficient to cover the whole of $\mathbb{P}^3$. It we conside the case of $\mathbb{P}^2$, the set of lines through the origin in $\mathbb{R}^3$, then every line will intersect one of three faces of the unit cube, $x=1$, $y=1$, or $z=1$. There is no need to find the intersection with the other three faces $x=-1$, $y=-1$, $z=-1$.

Once the four surfaces have been calculated they can be combined together to give a surface in $\mathbb{R}^4$. This surface can be rotated in 4D and projected to into 3D. First three rotations in 4D are applied $$ R_{xw}=\begin{pmatrix}\cos(\theta)&0&0&-\sin(\theta)\\0&1&0&0\\0&0&1&0\\\sin(\theta)&0&0&\cos(\theta)\end{pmatrix}, R_{yw}=\begin{pmatrix}1&0&0&0\\0&\cos(\phi)&0&-\sin(\phi)\\0&0&1&0\\0&\sin(\phi)&0&\cos(\phi)\end{pmatrix}, R_{zw}=\begin{pmatrix}1&0&0&0\\ 0&1&0&0 \\ 0&0&\cos(\psi)&-\sin(\psi)\\0&0&\sin(\psi)&\cos(\psi)\end{pmatrix}. $$ Then the points are projected to the lower half of the unit 3-sphere, $$(x,y,z,w)\to \frac{-\operatorname{sign} w}{\sqrt{x^2+y^2+z^2+w^2}}(x,y,z,w)$$ and finally a stereographic projection is applied mapping point on the 3-sphere to interior of the 3 sphere $$(x,y,z,w)\to\frac{1}{1-w}(x,y,z)$$.
The following figure shows the result of this algorithm, the colours represent which plane was used for the intersection. Note how the four surfaces knit together to form a surface which is smooth apart from at a the four nodes. The entire surface fits within the unit sphere and all four node always visable. The two projections only differ in the rotation in 4D.

Written by Richard Morris - rich@singsurf.org - Home Page
Last modified: April 4, 1997