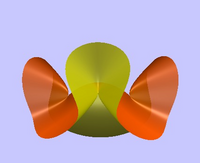
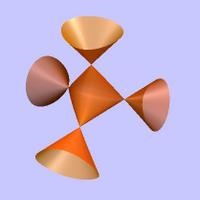Singularities of Cubic Surface

Cubic surfaces are implicit surfaces in projective three space with terms which are degree three or less. These surfaces can have several different types of singularity from the basic conical singularity A₁ to those containing a cross-caps and a line of nodal points.

Projective space

Cubic surfaces are defined in projective space which is a lot like normal 3D space, but which some extra structure at infinity. Points in projective 3 space are specified by 4 number, written (x:y:z:w), with an equivalence relation so that all non zero multiples of a point are considered equivalent. Hence, (ax: ay: az: aw)=(x:y:z:w) for all not zero a. In particular if w is not zero then (x:y:z:w)=(x/w:y/w:z/w:1) and dropping the final number projects this to normal R³ so (x:y:z:w) is projected to (x/w,y/w,z/w) allowing the surface to be view in three dimensions.

One way to think of the space is the set of lines through the origin in R⁴. If (x, y, z, w) is a points on such a line then so is (a x, a y, a z, a w) and the equivalence relation follows. Alternatively the space can be though of as the three sphere S³ with antipodal points identified.

For most of the surfaces below we have used a projection so that the points (1:0:0:0), (0:1:0:0), (0:0:1:0), (0:0:0:1) map to the vertices of a tetrahedron (1,1,1), (-1,-1,1), (1,-1,-1), (-1,1,-1). This is a particularly useful projection as the singularities of the expressions given by Cayley tend to lie at these four points.

Singularities

The type of singularity is determined by a classification due to Arnol'd, and are specified by their normal forms. In the complex case there is just one normal form for each, but in the real case changing the signs of the terms produce different images. Some of the alternate forms are shown, for many singularities one form is a single point, which is not shown.

Type	Normal form	Curve in 2D	Surface in 3D		Coxeter diagram
Simple singularities
A₁	x²+y²+z²
A₂	x³+y²+z²
A₃	x⁴+y²+z²
A₄	x⁵+y²+z²
A₅	x⁶+y²+z²
D₄	x³+x y²+z²
D₅	x⁴+x y²+z²
E₆	x³+y⁴+z²
Non simple singularities
Ẽ₆	x³+y³+z³ +k x y z

Coxeter–Dynkin diagram and the ADE classification

The various cubic surfaces can be characterised by their Coxeter–Dynkin diagram. These diagrams show the relationship between the generators of the Coxeter groups of symmetries, and are also used to describe the homology groups of cubic surfaces.

The Coxeter–Dynkin diagram of the different cubic surfaces are all derived from the diagram of the ${\tilde {E}}_{6}$ Affine Coxeter Group, by removing some of the edges.

Coxeter Dynkin diagram of the Affine E6 coxeter group

For example, and A1 singularity is represented by a single node and an A2 singularities is represented by a two nodes joined by a line. Hence for the Cubic with two A1 singularites and one A2 singularity is represented by the diagram

Cayley class XIII Coxeter Dynkin diagram

My page Singularities and the ADE classification tried to explain this characterisation in a visual manner.

The Cubic Surfaces

The following list of singularities follows Cayley. Schlafli was first to classify the various types. We use the modern notation for singularities following Bruce and Wall. Holzer and Labs distinguish between the different forms of the real singularities giving 45 types with rational double points.

Capitals X, Y, Z, W are used for coordinates in projective space and x, y, z for coordinates in R³.

Class I: No singularities

There are a number of well known non singular cubics.

Clebsch surface

This surface contain the maximum possible 27 real lines.

X³+Y³+Z³+W³-(X+Y+Z+W)³=0

One projection is 16 x³ + 16 y³ - 31 z³ + 24 x² z - 48 x² y - 48 x y² +24 y² z - 54 √3 z² - 72 z

Fermat Cubic

X³+Y³+Z³+W³=0

Ref: Wikipedia

Class II: one A₁ singularity

In Cayley's notation: C2

W (a X² + b Y² + c Z² + f X Y+ g X Z+h Y Z)+2 k X Y Z

Class III: one A₂ singularity

In Cayley's notation: B3

2W(X+Y+Z)(l X+m Y+n Z) + 2 k X Y Z

Some nice examples include

x z + y²(x+y+z)

By Bruce Hunt

S11

x²+y²+z³+3.2 (x³-3 x y²)

From University of Turin

Class IV: two A₁ singularities

In Cayley's notation: 2 C2

W X Z+Y²(k Z+l W)+a X³ +b X² Y+c X Y² + d Y³

Class V: one A₃ singularity

In Cayley's notation: B4

W X Z +(X+Z)(Y²-a X²-b Z²)

(x² + y²) w + 2 x (z² - 2 x² - 4 y²); w=1-y

Number KM26 in Holzer and Labs

Class VI: one A₁ and and one A₂ singularities

In Cayley's notation: B3+C2

W X Z+Y² Z+a X³ +b X² Y+c X Y² + d Y³

Class VII: one A₄ singularity

In Cayley's notation: B5

W X Z +Y² Z +Y X²-Z³

Class VIII: three A₁ singularities

In Cayley's notation: 3 C2

Y³+Y²(X+Z+W)+4 a X Z W

Cayley class VIII Coxeter Dynkin diagram

Class IX: two A₂ singularities

In Cayley's notation: 2 B3

W X Z+a X³+ b X² Y + c X Y² + d Y³

Class X: one A₁ and one A₃ singularities

In Cayley's notation: B4+C2

W X Z+(X+Z)(Y²-X²)

Class XI: one A₅ singularity

In Cayley's notation: B6

W X Z + Y² Z+X³- Z³

Class XII: one D₄ singularity

In Cayley's notation: U6

W(X+Y+Z)²+X Y Z

Two nice examples of the surface show the different real forms of the singularity.

S16

z² ( z + 4) + y (y - √3) x) ( y + √3 x)

From University of Turin

S17

z² ( z + 4) + y (x² + y²)

From University of Turin

Class XIII: two A₁ and one A₂ singularities

In Cayley's notation: B3+2 C2

W X Z+Y²(X+Y+Z)

Class XIV: one A₁ and one A₄ singularities

In Cayley's notation: B5+C2

W X Z+Y² Z+Y X²

Class XV: 1 D₅ singularity

In Cayley's notation: U7

W X²+X Z²+Y² Z

Class XVI: four A₁ singularities

In Cayley's notation: 4 C2

W(X Y+X Z+Y Z)+X Y Z

Cayley's Cubic

4 (x²+y²+z²) + 16 x y z - 1;

Cayley's expression X Y Z + X Y W + X Y W + Y Z W=0 has nodes at the four points (1:0:0:0), (0:1:0:0), (0:0:1:0) and (0:0:0:1) we can apply a rotation so that these points map to four verticies of cube center at (0:0:0:1), that is the points (1:1:1:1), (-1:-1:1:1), (1:-1:-1:1), (1:-1:-1:1), (-1:1:-1:1). Projecting these points to R³ via (x:y:z:w) → (x/w,y/w,z/w) gives vertices on a cube center origin. Plotting the resulting expression

X Y Z + X Y W + X Z W + Y Z W;
X = x + y + z + w;
Y = -x - y + z + w;
Z = x -y -z + w;
W = -x + y - z + w;
w = 1;

gives a surface where the nodal points are clearly visable.

-x² + z x² + y² z - 2 z³ + 3 z² - z;

A different projection of the same surface. From University of Turin

Class XVII: one A₁ and two A₂ singularities

In Cayley's notation: 2 B3 + C2

W X Z+X Y²+Y³

Cayley class XVII Coxeter Dynkin diagram

Class XVIII: two A₁ and one A₃ singularities

In Cayley's notation: B4 +2 C2

W X Z+(X+Z)Y²

Cayley class XVIII Coxeter Dynkin diagram

Class XIX: one A₁ and one A₅ singularity

In Cayley's notation: B6 + C2

W X Z + Y² Z + X³

Class XX: one E₆ singularity

In Cayley's notation: U8

W X² + X Z² + Y³

Class XXI: three A₂ singularities

In Cayley's notation: 3 B3

W X Z+Y³

Cayley 1

p₁ + (a₂z+a₃)p₃ + a₄ z³ + a₅z² + a₆ z + a₇;
p₁=2 x³-6 x y²;
p₃=x²+y²;
a₁ = -1; a₂ = -1; a₃=-3 a₁;
a₄ = 1; a₅=a₂²/(3 a₁);
a₆=-a₂; a₇=a₁;

Class XXII: two cross-caps and a nodal line

In Cayley's notation: S(1,1)

W X² + Z Y²

Class XXIII: nodal line

In Cayley's notation: S(1,1)

X(W X+Y Z)+Y³

References

Bruce, J. W.; Wall, C. T. C. (1979), "On the classification of cubic surfaces", The Journal of the London Mathematical Society. Second Series 19 (2): 245–256, doi:10.1112/jlms/s2-19.2.245, MR533323, ISSN 0024-6107 - Has details on the modern classification.
Cayley, Arthur (1869), "A Memoir on Cubic Surfaces", Philosophical Transactions of the Royal Society of London (The Royal Society) 159: 231–326, ISSN 0080-4614 - The classification this page is based on.
Holzer, Stephan; Labs, Oliver, "Illustrating the Classification of Real Cubic Surfaces" PDF - Visulise the 45 topological types for real cubic surfaces.
La collezione dei modelli di superfici del Dipartimento di Matematica dell'Università di Torino. (The Models of the Department of Mathematics University of Turin). Original page is dead, a mirror can be found at Gian Marco Todesco personal page. - A collection of 30 models originally done in plaster, cover many of the surfaces seen here.
H. Knörrer and T. Miller. Topologische Typen reeller kubischer Flächen. Mathematische Zeitschrift, 195, 1987. - Classification of the 45 real types.
Cubic surface home page - A website dedicated to cubic surfaces. Has images of each type.

3D Viewer-Generator

Your web browser must have JavaScript enabled in order for this application to display correctly.

Controls Java Version

Click image on left to load 3D model. Rotate with mouse, hold 's' and drag with mouse to scale, hold 't' and drag with mouse to translate.

3D surfaces are generated by the SingSurf algebraic surface program The raytraced images have been produced using Surf, using SingSurf and Javaview to select good views for raytracing.

Msqli defined

	Singsurf.org is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Based on a work at http://singsurf.org/parade/Cubics.php.
Yes this site uses cookies, mainly google analytics and google adsense. If thats a problem turn javascript off when browsing.

Singularities of Cubic Surface

Projective space

Singularities

Coxeter–Dynkin diagram and the ADE classification

The Cubic Surfaces

Class I: No singularities

Class II: one A1 singularity

Class III: one A2 singularity

Class IV: two A1 singularities

Class V: one A3 singularity

Class VI: one A1 and and one A2 singularities

Class VII: one A4 singularity

Class VIII: three A1 singularities

Class IX: two A2 singularities

Class X: one A1 and one A3 singularities

Class XI: one A5 singularity

Class XII: one D4 singularity

Class XIII: two A1 and one A2 singularities

Class XIV: one A1 and one A4 singularities

Class XV: 1 D5 singularity

Class XVI: four A1 singularities

Class XVII: one A1 and two A2 singularities

Class XVIII: two A1 and one A3 singularities

Class XIX: one A1 and one A5 singularity

Class XX: one E6 singularity

Class XXI: three A2 singularities

Class XXII: two cross-caps and a nodal line

Class XXIII: nodal line

References

3D Viewer-Generator

Class II: one A₁ singularity

Class III: one A₂ singularity

Class IV: two A₁ singularities

Class V: one A₃ singularity

Class VI: one A₁ and and one A₂ singularities

Class VII: one A₄ singularity

Class VIII: three A₁ singularities

Class IX: two A₂ singularities

Class X: one A₁ and one A₃ singularities

Class XI: one A₅ singularity

Class XII: one D₄ singularity

Class XIII: two A₁ and one A₂ singularities

Class XIV: one A₁ and one A₄ singularities

Class XV: 1 D₅ singularity

Class XVI: four A₁ singularities

Class XVII: one A₁ and two A₂ singularities

Class XVIII: two A₁ and one A₃ singularities

Class XIX: one A₁ and one A₅ singularity

Class XX: one E₆ singularity

Class XXI: three A₂ singularities