Here we will attempt to explain the connection between the classification of singularities and the ADE classification of Coxeter groups.
The best explanation I've found for this is Joris van Hoboken's Masters Thesis Platonic solids, binary polyhedral groups, Kleinian singularities and Lie algebras of type A,D,E (University of Amsterdam, 2002)
The basic idea is of blowing up singularities, this replaces each A1 singular point by a circle creating a smooth surface. Higher singularities have more complex blowups, A2 blows up to two linked circles, A3 to three circles, D4 to three circles all linked to a common fourth circle.
Calculating the homology group of this resulting surface allows the different types of singularity to be identified. These homology groups also link into the Coxeter Dynkin diagrams and the ADE classification.
The goal of a resolution of a singularity is replacing a surface $V$ with singularity by another surface $U$ which is non-singular and away from the singular point is the same (isomorphic). To get a resolution we use a technique called a blow-up, this replaces the singular point by a line.
Consider this map from a cylinder to an A1 singularity.
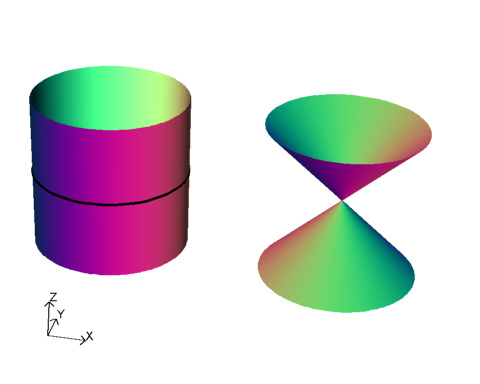
The cylinder is defined as $x^2+y^2=1$ and the map $\mu: (x,y,z) \to (x z, y z,z)$ produces the A1 singular surface $x^2+y^2-z^2=0$. The circle $x^2+y^2=1, z=0$ is sent to the singular point and is called the exceptional set. Away from the circle the map is 1 to 1 and onto.
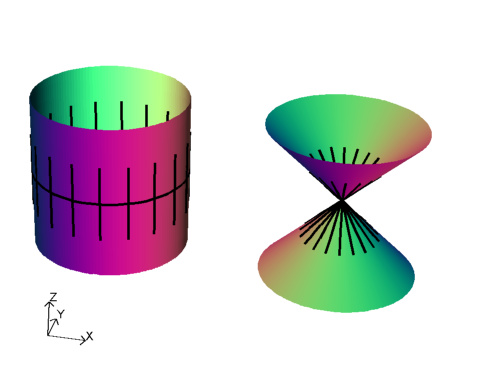
One particular feature of this map is if you take lines that cross the circle they map to lines that pass through the singularity.
So we can thing of replacing the singularity by the set of lines passing through it.
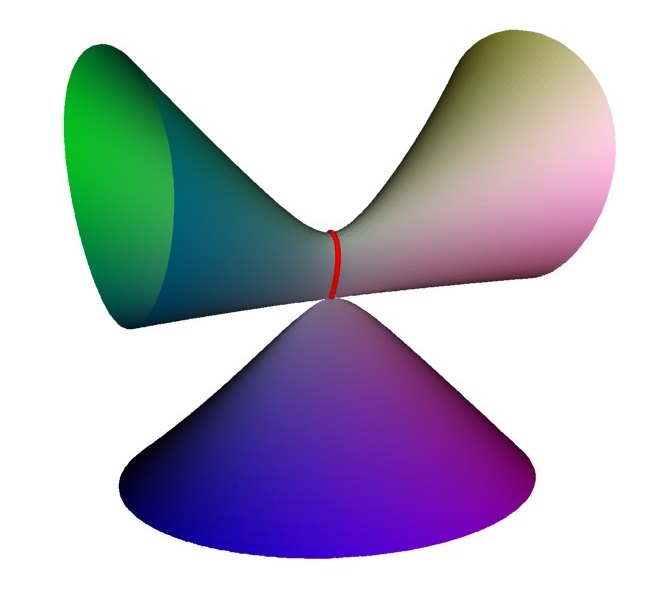
A related concept is unfolding. Here we consider our singular surface as part of a family of surfaces, most of which are not singular. For the A1 singularity $x^2 + y^2 - z^2 =0$ we can consider the family $x^2 + y^2 - z^2 + d=0$ for different values of $d$.
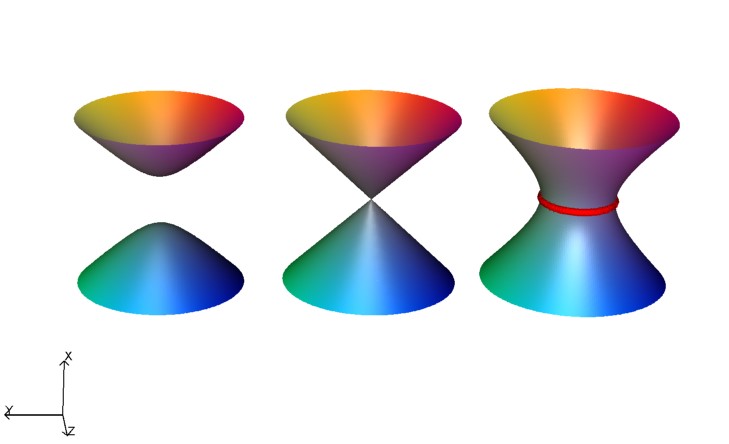
Note that the right hand surface above is topologically the same as the blowup of the singularity. In particular both have one loop round the surface. In this hand-wavy explanation we blur the distinction between resolutions, blow-ups and unfoldings.
To represent these of the Coxeter-Dynkin diagram we can replace a solid circle with an open circle.
The A2 singularity is represented by Coxeter-Dynkin diagram with
two linked nodes.

3D Model: A2 singularity
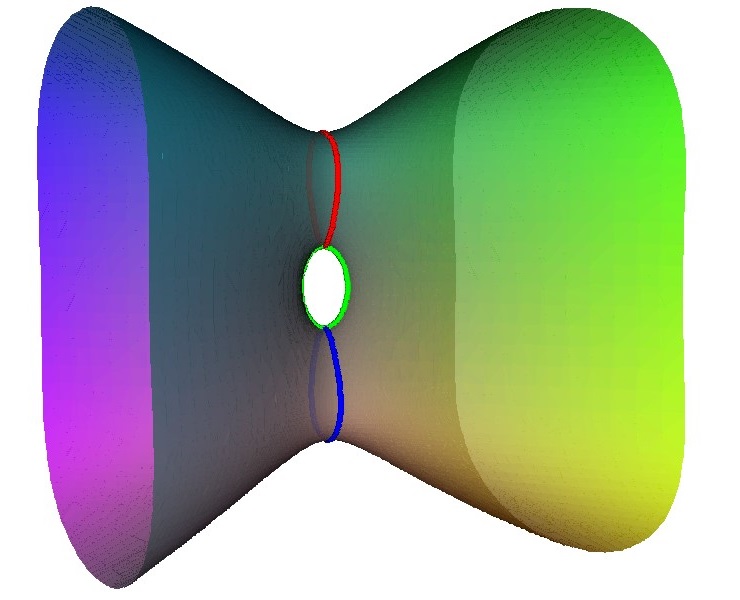
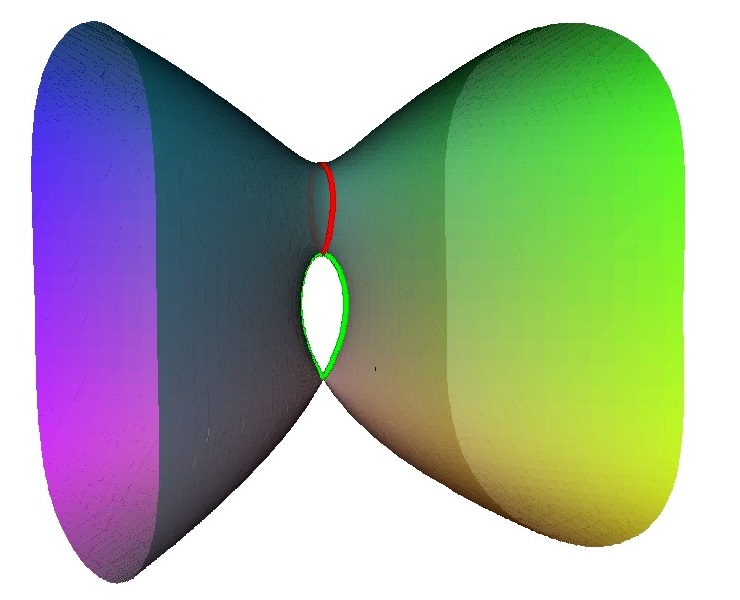
To see how this comes about consider this unfolding of an A2 singularity. It happens in two stages, first a loop is created with an A1 point on it. Then this A1 point is unfolded to form a second loop.



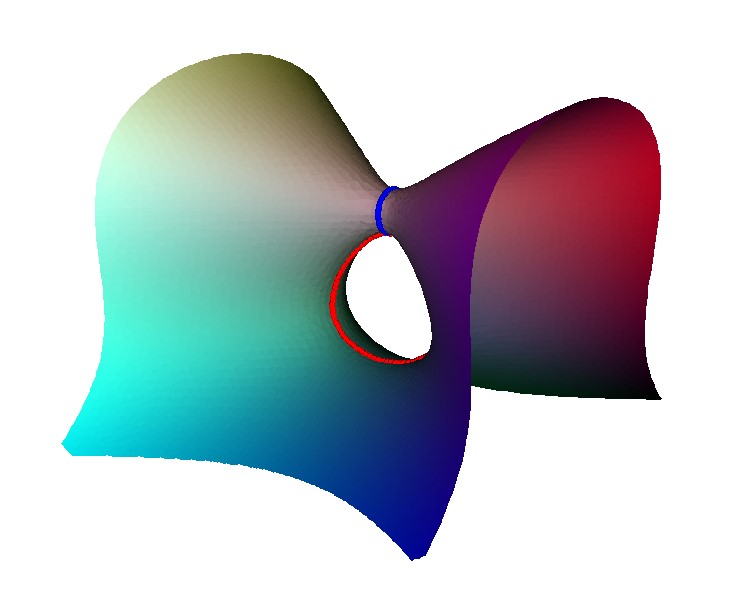
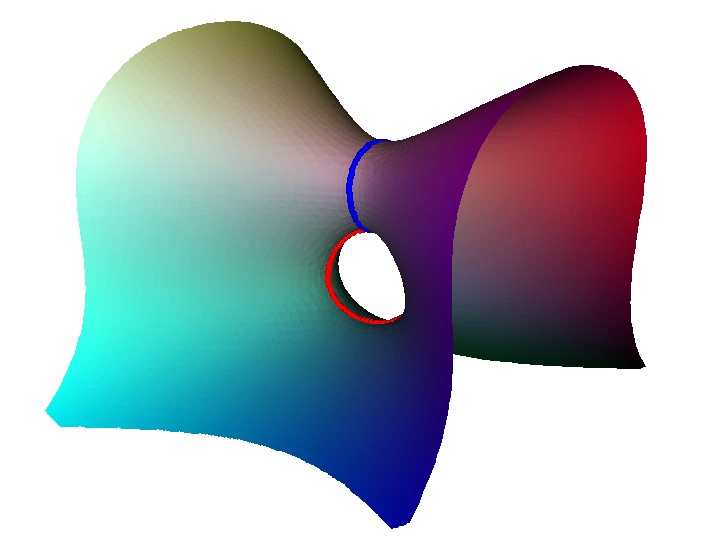
The result of the unfolding give two linked loop. Each of these corresponds to a node on the Dynkin diagram, and as they are linked there is an edge in the Dynkin diagram.
3D Model: Unfold stage 1
3D Model: Unfold stage 2
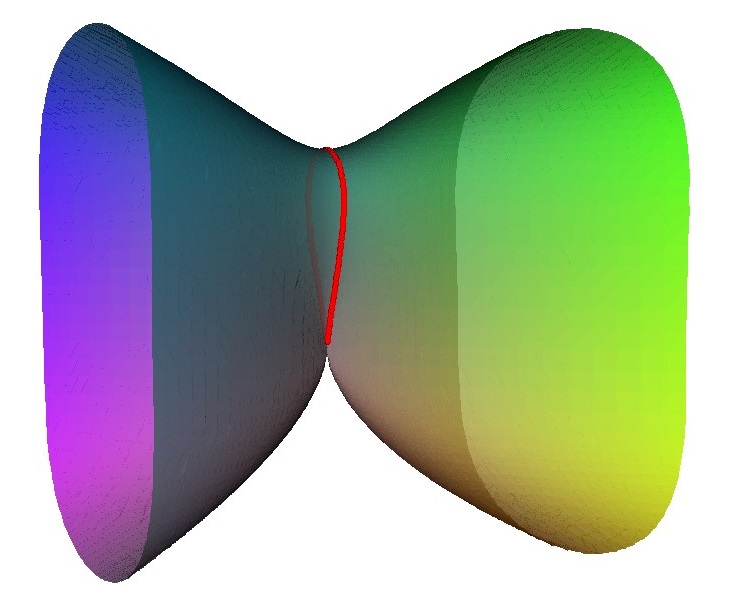
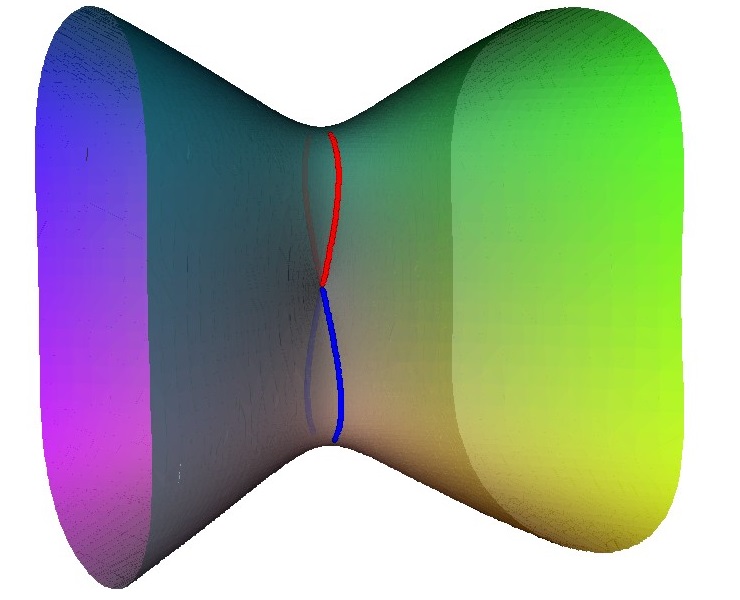
For the A3 singularity there is similar pattern the singularity can be unfolded to three linked loops. There are various intermediate states with either an A2 singularity; two A1 singularities or a single A1 singularity.
|
|
||
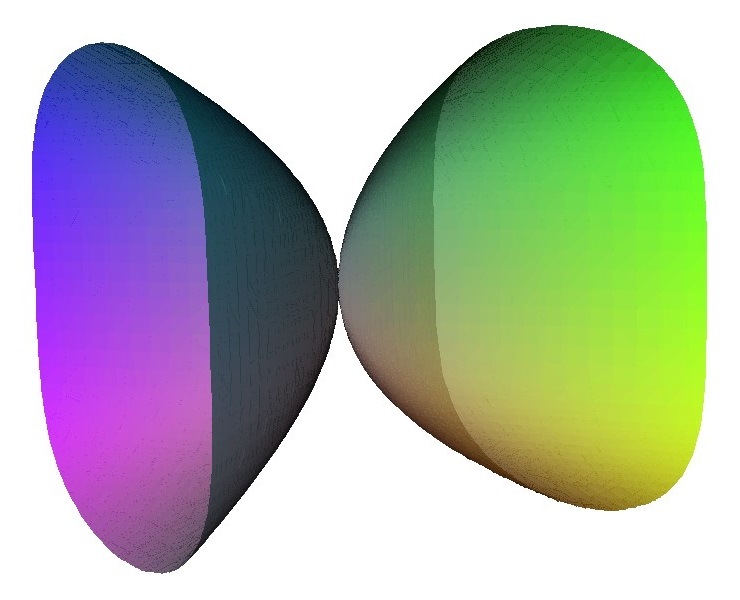
|
|
||
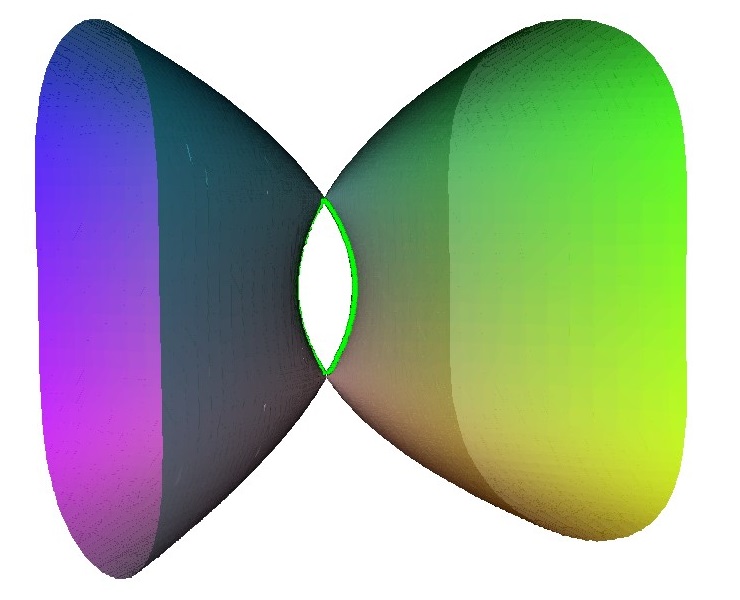
|
|
The D4 singularity is the first one where the Coxeter-Dynkin diagram has a branch: .

3D Model: unfolded D4 singularity
The first stage of unfolding can occur in two different ways. One equivalent to removing the central node, giving rise to a shape with 3 A1 singularities. Alternatively one of the outer nodes can be removed, leaving an A3 singularity. Here we have used the unfolding $x^2 y - y^3 - z^2 + a ( y^2 + x y) + b y^2$, $a=b=0$ give the singularity changing the $s$ parameter gives the 3 A1 configuration going top to bottom, and change $b$ give the left-right configuration.

|
||
|

|

|

|
The full unfolding of the singularity is complex, and includes members with 2 A1 singularities, and one A1 singularity.

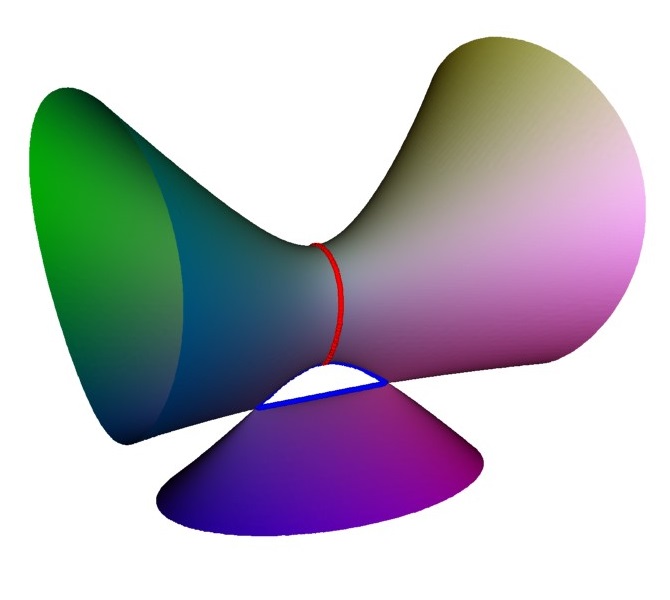
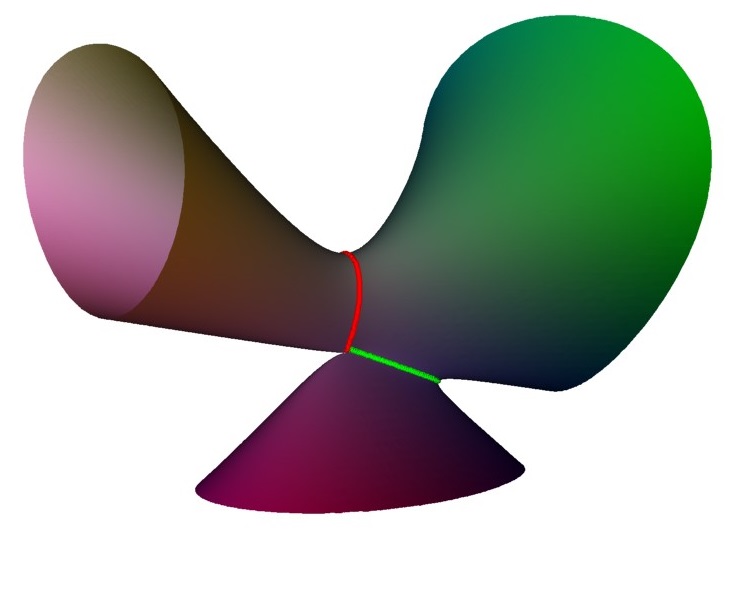
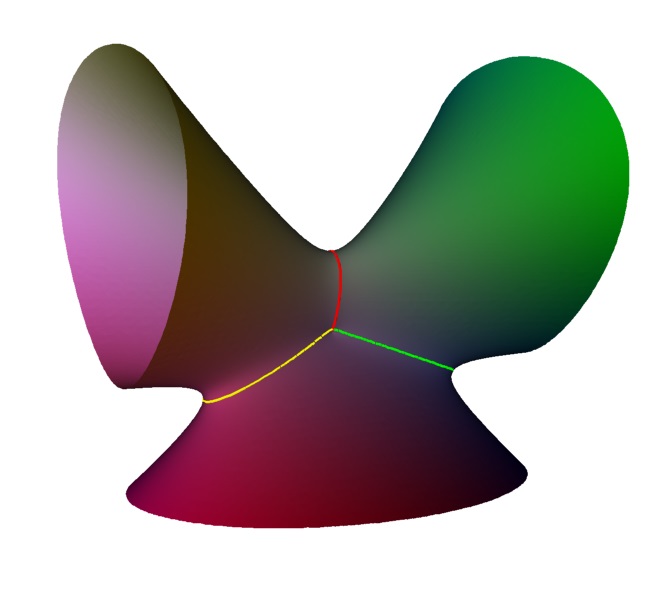

Here is one
non-singular member showing four linked loops. Note how the central blue loop
has points in common with each of the other loops, corresponding
to a line joining them in the Coxeter-Dynkin diagram. But the
other pairs have no point in common, hence no line in the diagram.
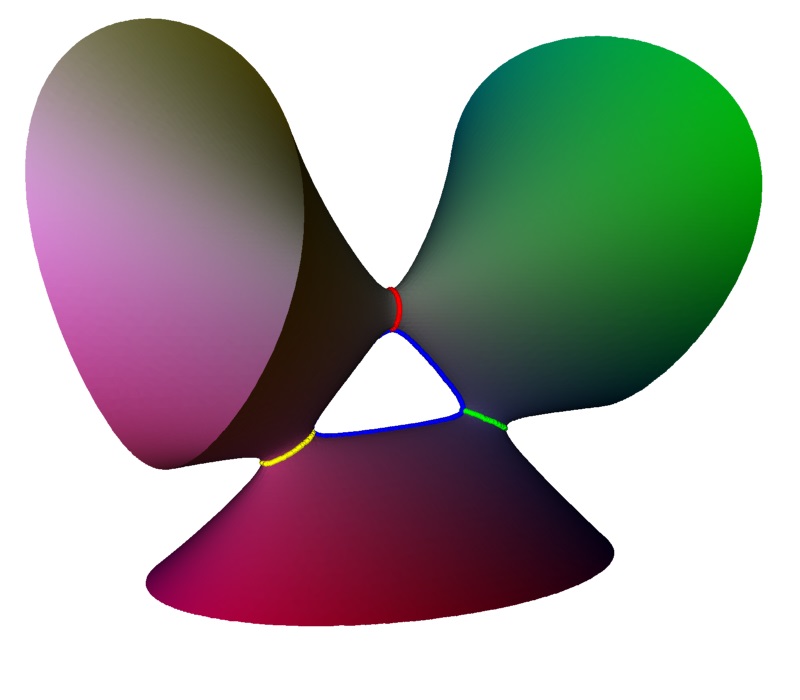

3D Model: unfolded D4 singularity
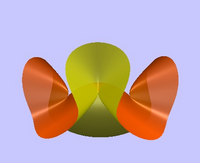
The Affine Coxeter Group ${\tilde {E}}_{6}$ corresponds to the cubic surface $x^3+y^3+z^3+k x y z$, this can have multiple forms depending on the parameter $k$.


The has Coxeter–Dynkin diagram
All the Cubic surfaces occur in the unfolding of ${\tilde {E}}_{6}$ there are 23 different types in Cayley's classification, including the A1, A2, A3 and D4 singularities above and all their unfoldings; the A4, D5 and E6 singularities; surfaces with multiple nodes, like Cayley's cubic with 4 A1 singularities; and surfaces with nodal lines, S(1,1).
| Multiplicity | Surface | Diagrams | |
|---|---|---|---|
| 7 |

|
${\tilde {E}}_{6}$ |
|
| 6 |


|
$E_6$ |
|
| 5 |





|
$D_5$ |
|
| 4 |






|
$D_4$ |
|
| 3 |



|
$A_3$ |
|
| 2 |


|
$A_2$ |
|
| 1 |

|
$A_1$ |
|
| 0 |

|