
The following has largely been taken from an answer to a question on Quora looking for a simple explination to the shape sometimes seen in the bottom of a teacup.
For $\not 3 Q \not B$ a high level explanation we can look to Catastrophe theory this theory describes the local behaviour of maps and finds common patterns. Consider a map from the plane to the plane. For $s$, $t$ real number $M(s,t)$ gives a point in the plane. (so this is a bit like a function with 2D output).We can describe the rays of light by such a map, for a particular ray let $t$ be the time from the light source, effectively the distance from the light source. The other parameter s gives the particular ray, for a point source this might be the angle the ray left the source. Fixing $s$ then $M(s,t)$ describes the path of the ray.
Lets impose some restrictions on the map so that it has no sudden jumps (continuous) and also all its derivatives exist (smooth). Away from the edges of the coffee cup our map of light rays satisfies this.
Now define the two coordinate functions $f$, $g$ with $M(s,t)=(f(s,t),g(s,t))$ and consider the matrix of partial derivatives
\[\begin{pmatrix} \frac{\partial f}{\partial s}&\frac{\partial f}{\partial s}\\ \frac{\partial g}{\partial s}&\frac{\partial g}{\partial t} \end{pmatrix}\]called the Jacobian matrix. If this is non-singular then the Map is said to be non singular - its well behaved and is approximately like the identity map (after rotations, scaling etc). This is the normal behaviour away from the edge of the caustic. Now things get interesting if the matrix is singular and we see the different elementary catastrophies of Rene Thom appearing.
The simplest of these is the fold catastrophe. The simplest example of this is the map $M(s,t)=(s,t^2)$ where all points map to the upper half plane. An example closer to out situation is $M(s,t)=(s + t, s t)$ note that for a fixed s this describes a straight line which is what a light ray should do.
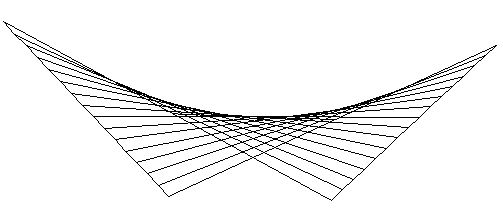
The map $(s+t,s t)$ showing the rays for different values of $s$. If we look at the matrix of partial derivatives we see that it is $\begin{pmatrix} 1 & 1 \\ 0 & 0\end{pmatrix}$ clearly singular.
The next most complex catastrophe is the cusp, here an example is $(s^2 + t, s t)$ again the matrix of first derivatives is singular and there are also conditions of the second derivative.
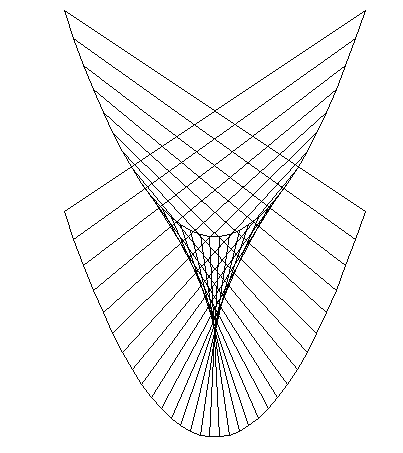
It is a cusp map you are seeing in the coffee cup.
There is a lot of high power mathematical machinery which shows these are the two simplest examples and furthermore you would expect these to occur, rather than other patterns (unless you are dealing with a particular rare case).
You could do the sums, find out the equations of the light rays reflected by a circular cup. Find the caustic by finding where the matrix of first derivatives vanishes. Its a little messy but possible.