Nice
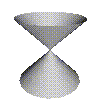Weird
You can have a look at some bigger pictures of these: nice surface, weird surface, and also some 3D models (9K each): nice surface, weird surface.
Well, one is nicely behaved and the others a bit weird, but what do we mean precisely?
Technically we say the one on the left is smooth and the one on the right is singular. Formally the definition of smooth and singular depend on derivatives, and we'll look at that later in A parade of Surfaces. For now we'll try to get an intuative definition by looking at tangent planes.
First lets consider a curve.
At any point on the curve we can find a line which just touches the curve, but does not cross the curve. Such lines are said to be tangent to the curve, lines which cross the curve are called transverse. For example,
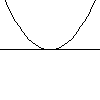tangent
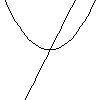transverse.
Any point on this curve, has a unique tangent. Occasionally you can have inflections on curves where the curve changes from turning one way to turning the other way.
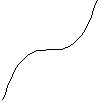inflection
Here the tangent does cross the curve, but it still makes a zero angle
tangent
Now we get to the crunch, not all curves have unique tangents. For this curve, we have two posibilities for the tangent,
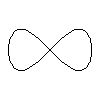curve
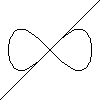tangent 1
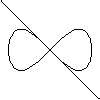tangent 2.
Curves where we do not have a unique well defined tangent are called singular. There are other curves which do not have a well defined tangent for instance a cusp,
cusp.
You might think that the horizontal line would be a tangent in this case, but a strict mathematical definition says that no tangent is defined in this case. Intuativly you can think that if we move from top to bottom along the curve, then the we first move down and to the left, at the cusp point we flip round and start moving down and to the right. When ever we flip directions like this we don't have a proper tangent, and the curve is called singular.
If you want to find out a little more about how we find the tangent line, and a more percise definition of what we mean when we say a tangent line is well defined, you can follow this link about limiting tangents.
We can use the same idea to look at surfaces. Remember the nice surface we had,
nice surface.
nice surface.
big picture (13K)
3D model (10K).
Note this picture was created by using the Rayshade package, which does quite a good job of simulating real lighting, notice the shadows.
But what about the weird surface?
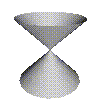Weird
What the tangent plane at the middle? Well theres a whole number of posible candidates, for instance
tangent?
big picture (11K)
3D model (7K).
We could rotate the plane around the surface to get another tangent plane which is just as good as this one. Hence we can conclude that this surface does not have a unique, well defined tangent plane. Therefor this surface is singular.
Before we go on theres another nice surface, which looks a little different to the first one we saw.
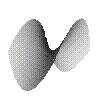nice surface.
big picture (13K)
3D model (10K).
Here the tangent plane cuts the surface in two lines, but it is still well defined.
tangent?
big picture (13K)
3D model (9K).
Incidentally the way the tangent plane cuts the surface gives us a clasification of nice points. The first type where the tangent plane cuts the surface in a single point is called an elliptical point, and the other type where the tangent plane cuts the surface in two curves is called a hyperbolic point. In fact thers another type where the tangent plane cuts the surface in a cusp shape, which is called a parabolic point. The names come from the ellipse and hyperbola which you might have met elsewhere. Just think of moving the tangent plane down a little, in one case the tangent plane would cut the surface in an ellipse, in the other case it cut in a hyperbola.
Now we've seen that having a well define tangent line or plane tells us whether the surface is singular or not, you can take a look again at When things go weird and convince you self that none of the weird surfaces have well defined tangent planes.
