Nice 
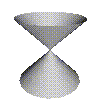Weird
You can have a look at some bigger pictures of these: nice surface, weird surface, and also some 3D models (9K each): nice surface, weird surface.
In singularity theory we look at the different types of weird surface. In the later sections we'll give a precise definition of what we mean by weird. For now we'll just say if a surface is nicely behaved its called smooth but if its not well behaved its called singular. The surface on the left is nicely behaved at all points and its smooth everywhere. The surface on the right is only singular at one point, right in the middle, at all the other points its smooth.
Of course not all weird surfaces are the same have a look at this one:
and this one:
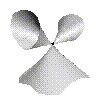Big picture,
3D model (28K),
3D model (74K)
and one of my favorites:
big picture,
threeD model (17K),
three D model (49K)
All these surfaces are very different but it can be quite difficult to describe what is different about them. One of the tasks of singularity theory is to produce lists of different types of singularities, we'll go into the detail of how we do this later. The three above have types A3, D4, and E7, not the most exciting of names.
Sometimes you can have more than one singular point:
big picture,
threeD model (22K)
This ones got 12. Infact you can have lots and lots this one:
has 65 singularities which is a world record number of singularities for an sextic equation, (i.e. an equation involving terms of degee 6, like x^6 or x^2 * y^2 * z^2, you don't need to worry about this). I'm afraid that theres no 3D model for this one as its half a megabyte big.
Things get even stranger when we have cuspidal edges which looks like
big picture (10K),
threeD model (2K)
Here we have singular points all the way along a line.
For maximium weirdness you can have even stranger singularities which occur on lines on cuspidal edges, for instance the swallowtail.
big picture (8K),
threeD model (46K)
It's called a swallowtail because one of the edges of the curve looks a bit like a swallow's tail.
It quite a big problem in maths to come up with good names for surfaces, this one's called a whitney umbrella,
big picture (9K),
threeD model (2K)
although its probably not that good for keeping the rain out. Depending on the way its defined the umbrella can either have a handle or not. When it does not have a handle some people call it a cross-cap or pinch-point.
