Construction the skeleton of a singularity

Skeletons for nodes

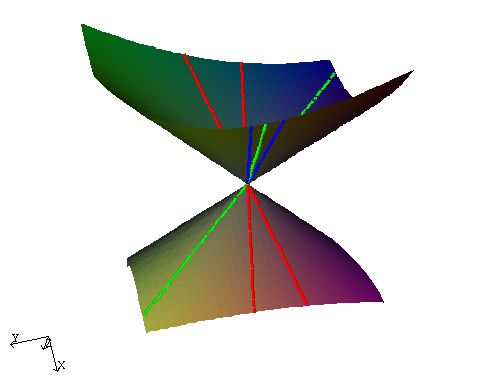
In the normal form of an A1 singularity, $F(x,y,z)=x^2+y^2-z^2$, two of the three partial derivatives $\frac{\partial F}{\partial x} = 2 x$ (in red), $\frac{\partial F}{\partial y} = 2 y$ (in green), $\frac{\partial F}{\partial z} = 2 z$ (in blue), intersect the surface in pairs of lines passing through the singular point.

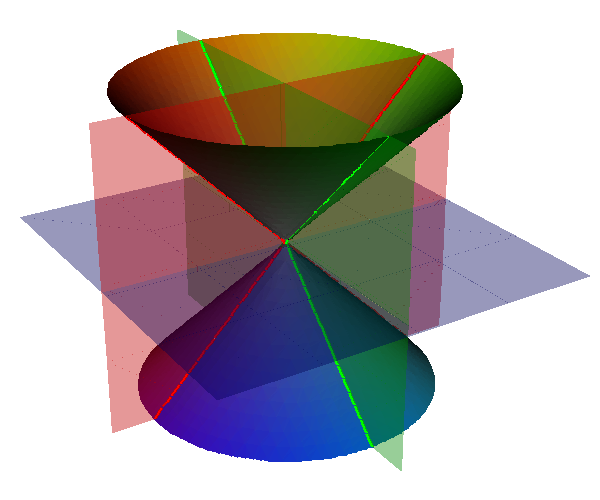
Normal form of A1 singularity with derivative
Normal form of A1 singularity with derivative, showing the three partial derivatives and the skeleton consisting of the intersection of the partial derivatives with the surface

We can use the intersection of the surface with the three partial-derivative surfaces to help triangulate the surface. As all three derivatives vanish at a singularity we know that the partial derivative surfaces and hence the intersections will pass through the any singularities.

Definition
The skeleton of an implicit curve is the union of the three varieties $\mathbf{V}\left(F,\frac{\partial F}{\partial x}\right)$, $\mathbf{V}\left(F,\frac{\partial F}{\partial y}\right)$, $\mathbf{V}\left(F,\frac{\partial F}{\partial z}\right)$. The skeleton is further divided into three sets x-skeleton: $\left\{(x,y,z) : F(x,y,z)=0, \frac{\partial F}{\partial x} = 0\right\}$, y-skeleton: $\left\{(x,y,z) : F(x,y,z)=0, \frac{\partial F}{\partial y} = 0 \right\}$, z-skeleton: $\left\{(x,y,z) : F(x,y,z)=0, \frac{\partial F}{\partial z} = 0 \right\}$.

Including points on the skeleton help produce a good polygonization around the singular point.

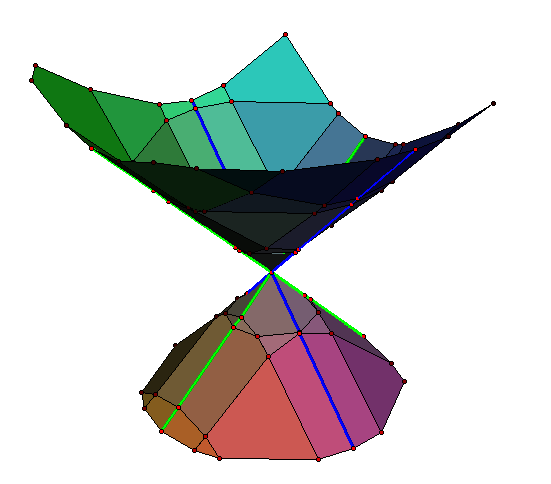
Skeleton of A1 singularity
Polygonization of A1 singularity showing how points on the skeleton can produce a improved polygonization.

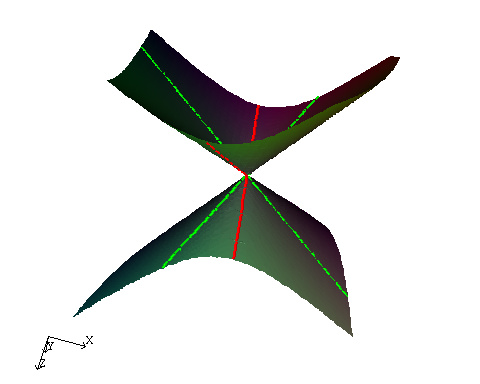
For the A1 normal form two sets of edges of the skeleton pass through the singular point, but is this always the case? If we rotate the surface and then calculate the partial derivatives are there always parts of the skeleton that pass through the singular points?

It turns out that this is not always the case. It is possible to find varities where either 0, 1, 2 or 3 of the partial derivatives form part of the skeleton.

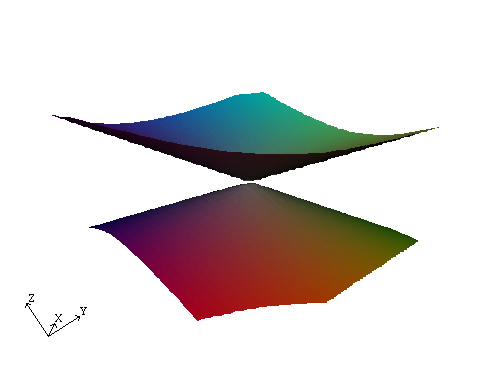
A1 singularity with no derivative
Fig 3a) A1 singularity where the x-skeleton, y-skeleton and z-skeleton all consist of a single point at the singularity. $-0.46 x^2-0.26y^2-1.88z^2$ $-1.68 x y-2.90 x z -2.62 y z $
A1 singularity with 1 derivatives
Fig 3b) A1 singularity where just the x-skeleton has two branches $+0.05 x^2-0.26 y^2-1.88 z^2$ $-0.90 x y-2.54 x z-2.62 y z$
A1 singularity with 2 derivatives
Fig 3c) A1 singularity where the x-skeleton and y-skeleton both have two branches. $+1.0 x^2+0.19 y^2-1.25 z^2$ $+0.20 x y-0.7 y z-1.0 x z$
A1 singularity with 3 derivatives
Fig 3d) A1 singularity where all three parts of the skeleton have two branches $0.05x^2+0.97 y^2+0.01 z^2$ $-2.22 x y -3.7 x z+0.02 y z$
Drawing the derivative planes show none of them intersect the surface away from the singularity.
A1 singularity with no derivative
A1 singularity where the skeleton just has a single point, showing the three derivative planes $\frac{\partial f}{\partial x} = 0, \frac{\partial f}{\partial y} = 0, \frac{\partial f}{\partial z} = 0$, none of which intersect the surface other than at the singularity.

Quadratic forms

$F(x,y,z)$ can be treated as ternary quadratic form. If $F$ is positive definite or negative definite then $F(x,y,z)\ne 0$ for all $(x,y,z)\ne 0$, and the surface consists of a single isolated point. If the matrix of coefficients $M$ has determinant zero the quadratic form is degenerate and the surface consists or two intersecting planes. Hence we are only interested in non-degenerate indeterminate forms, that have signatures +1 or -1.

If $M$ is positive definite then $a\gt 0, d\gt 0, f\gt 0$. By the Sylvester's criterion its necessary and sufficient that $a\gt 0$, $a d - b^2 \gt 0$, $|M|\gt 0$.

If $M$ is negative definite then $a\lt 0, d\lt 0, f\lt 0$. its necessary and sufficient that $a\lt 0$, $a d - b^2 \gt 0$, $|M|\lt 0$.

Impact on the algorithm

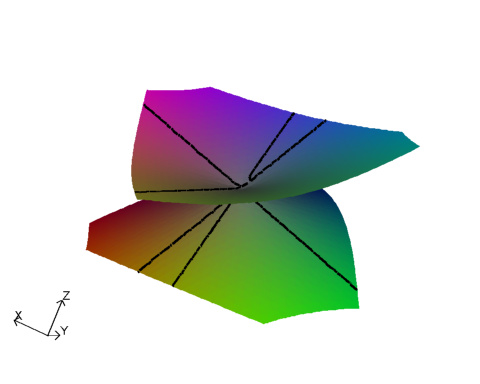
The case where none of the derivative planes intersect poses problems for the algorithm. Normally the algorithm find the intersection of the surface with the boundary of a box and also any singular points inside the box. It then attempts joining points on the boundary to the singularity along parts of the skeleton. When the skeleton is empty this is not possible and the singularity is not correctly linked, note how in the image above with zero derivative the surfaces does not contain the singular point, instead it has two disconnected components.

This problem can be overcome by notionally rotating the surface, calculating derivatives, and then rotating back. This is equivalent to calculating the intersection with surfaces like $\frac{\partial f}{\partial x} - \frac{\partial f}{\partial x} = 0$,

A1 singularity with no derivative
A1 singularity with no derivative, and intersections with $\frac{\partial f}{\partial x} -\frac{\partial f}{\partial y} = 0$, and $\frac{\partial f}{\partial x} -\frac{\partial f}{\partial z} = 0$.

With this enhanced skeleton, consisting of intersections with nine surfaces, $\frac{\partial f}{\partial x}=0$, $\frac{\partial f}{\partial y} = 0$, $\frac{\partial f}{\partial z} = 0$, $\frac{\partial f}{\partial x} \pm\frac{\partial f}{\partial y} = 0$, and $\frac{\partial f}{\partial x} \pm\frac{\partial f}{\partial z} = 0$, and $\frac{\partial f}{\partial y} \pm\frac{\partial f}{\partial z} = 0$ it should hopefully always produce sufficient segments to nicely triangulate an A1 singularity.

Conditions for point on a skeleton

Consider the variety $F(x,y,z) = a x^2 + 2 b x y + 2 c x z + d y^2 + 2 e y z + f z^2 = 0$, the three partial derivative are $\frac{\partial F}{\partial x} = 2 a x + 2 b y + 2 c z$, $\frac{\partial F}{\partial y} = 2 b x + 2 d y + 2 e z$, $\frac{\partial F}{\partial z} = 2 c x + 2 e y + 2 f z$. To find the x-skeleton, with $\frac{\partial F}{\partial x}=0$, substitute $y = -\tfrac{a}{b}x -\tfrac{c}{b}z$, with $b\ne0$, into $F=0$ giving $$a x^2 + 2 b \left(-\tfrac{a}{b} x - \tfrac{c}{b} z\right) x + 2 c x z + d \left(-\tfrac{a}{b} x - \tfrac{c}{b} z\right)^2 + 2e \left(-\tfrac{a}{b} x - \tfrac{c}{b} z\right) z + f z^2=0.$$ Multiply through by $b^2$ and find the coefficients of the quadratic in $x$ and $z$, $$(a^2 d - a b^2 ) x^2 + 2 (a c d - a b e ) x z + ( b^2 f - 2 b c e + c^2 d ) z^2=0.$$ The discriminant is $$\begin{align} 4 &( a c d - a b e )^2 - 4 (a^2 d - a b^2 )( b^2 f - 2 b c e + c^2 d ) \\ &= 4 a b^2 (-a d f + a e^2 + b^2 f - 2 b c e + c^2 d) \\ &=-4 a b^2 |M|\end{align}$$ Divide by the square term and set $\Delta_x = -a\ | M |$. The x-skeleton will have two branches if $\Delta_x\gt0$, a degenerate line when $\Delta_x=0$ and have just a single point if $\Delta_x\lt 0$. $\Delta$ changes sign when either the $a$ or the determinant changes sign. There are similar conditions $\Delta_y=-d\ |M|\gt0$, $\Delta_z=-f\ |M|\gt0$, for whether the y-skeleton and z-skeleton respectively have branches.

In Figure 3 above all cases has $|M|\lt0$, in Fig 3a, $a\lt0, d\lt0,$ and $f\lt0$ so $\Delta_x \lt0, \Delta_y\lt0$, and $\Delta_z\lt0$ and the x-skeleton, y-skeleton and z-skeletons all consist of a single point. The other cases show the effect of $a$, $d$ and $f$ changing sign.

A1 singularity with no derivative
Quadratic surface where $|M|=0$

Next consider the variety $V\left(F=0, \frac{\partial F}{\partial x} + \frac{\partial F}{\partial y}=0\right)$ $$\frac{\partial F}{\partial x} - \frac{\partial F}{\partial y} = 2(a x + b y + c z) - 2(b x + d y + e z) = 2(a-b)x + 2(b-d)y + 2(c-e)z.$$ Assume $e-c\ne 0$ and set $z = \frac{a-b}{e-c} x + \frac{b-d}{e-c}y$, substitute into $F=0$ $$a x^2 + 2 b x y + 2 c x \left(\frac{a-b}{e-c} x+\frac{b-d}{e-c} y\right) + d y^2 + 2 e y \left(\frac{a-b}{e-c} x+\frac{b-d}{e-c} y\right) + f \left(\frac{a-b}{e-c} x+\frac{b-d}{e-c} y\right)^2 $$ multiply through by $(e-c)^2$ $$a (e-c)^2 x^2 + 2 b (e-c)^2 x y + 2 c (e-c) x \left((a-b) x+(b-d) y\right) + d (e-c)^2 y^2 + 2 e (e-c) y \left((a-b) x+(b-d) y\right) + f \left((a-b) x+(b-d) y\right)^2 $$ expand and collect terms $$\begin{align} &( -2 a b f+a e^2+a^2 f+2 b c^2+b^2 f-a c^2-2 b c e) x^2 \\ &+ ( 2 a b f+2 a e+2 b d f+2 b e^2+2 c^2 d-2 a d f-2 b c e-2 b e-2 b^2 f-2 c d e ) x y\\ &+ (-2 b d f+2 b e+b^2 f+c^2 d+d e^2+d^2 f-2 c d e-2 d e ) y^2 \\ &= 0 \end{align}$$ the descriminant is $$ \begin{align} (&2 a b f+2 a e+2 b d f+2 b e^2+2 c^2 d-2 a d f-2 b c e-2 b e-2 b^2 f-2 c d e )^2 \\ &\quad- 4 ( -2 a b f+a e^2+a^2 f+2 b c^2+b^2 f-a c^2-2 b c e) (-2 b d f+2 b e+b^2 f+c^2 d+d e^2+d^2 f-2 c d e-2 d e ) \\ & = -4 (a + d - 2 b) (e-c)^2 ( a d f + 2 b c e - a e^2 - d c^2 - f b^2) \\ & = -4 (a + d - 2 b) (e-c)^2 | M| \end{align} $$ Set $\Delta_{x-y} = - (a + d - 2 b) |M|$, similar expressions can be used to check other parts Set $\Delta_{x+y} = - (a + d + 2 b) |M|$, Set $\Delta_{x-z} = - (a + f - 2 c) |M|$, Set $\Delta_{x+z} = - (a + f + 2 c) |M|$, Set $\Delta_{y-z} = - (d + f - 2 e) |M|$, Set $\Delta_{y+z} = - (d + f + 2 e) |M|$, even this set does not always produce non trivial skeletons. With $a=-0.2, b =0.1, c=-0.5, d=-0.46, e=0.26, f=-0.10$ All the varieties above are trivial.

Next consider the variety $V\left(F=0, \frac{\partial F}{\partial x} + \frac{\partial F}{\partial y} + \frac{\partial F}{\partial z}=0\right)$ $$ \begin{align} \frac{\partial F}{\partial x} + \frac{\partial F}{\partial y} + \frac{\partial F}{\partial z} &= (2 a x + 2 b y + 2 c) + (2 b x + 2 d y + 2 e z) + (2c x + 2 e y + 2 f z) \\ &= (2 a + 2 b + 2 c) x + (2 b + 2 d + 2 e) y + (2 c + 2 e + 2 f) z \end{align}$$ set $z= \frac{-1}{2 c + 2 e + 2 f} ( (2 a + 2 b + 2 c) x + (2 b + 2 d + 2 e) y )$ substitute into $F$ and calculating the discriminant we obtain the condition $\Delta_{x+y+z} = - (a+d+f+2b+2c+2e) |M|$. $\Delta_{x+y-z} = - (a+d+f+2b-2c-2e) |M|$. $\Delta_{x-y+z} = - (a+d+f-2b+2c-2e) |M|$. $\Delta_{x-y-z} = - (a+d+f-2b-2c+2e) |M|$. This still fails with $a=-0.23, b=0.49, c=-0.41, d=-0.95, e=0.78, f=-0.63$ all above test fails.

Msqli defined