Lets start with an image

and consider a reflection

Each reflection is represented by a point in the Coxeter-Dynkin diagram.
So a single reflection will be represent by just a single point.
Next consider two reflections with their mirrors at right-angles

if you do one followed by the other
you get a rotation by 180°. If you do this twice you get back to the
beginning, so the combined operation has order 2.
This is the typical arrangement so for the CD diagram we just draw
this as two points without a line between them.
What if the two reflections are at 60° then performing the reflections one after the other gives a rotation by 120° this has order 3. You also get a third reflection (in yellow) by doing the first reflection, then the second and then the first reflection again.

An important point is the difference between elements and generators
of the group. For the 60° reflection there are six elements in the
group:
the identity, reflection about 0° (in blue), reflection about +60° (in green), reflection
about -60° (in yellow), rotation +120° rotation of -120°. Two of the reflections
are chosen as generators as the third can be found by combining the other two.
In the CD has two points with a single line joining them.
If they are at 45° then the two reflections can be combined to give two other reflections (in yellow and orange) and rotations by 90°, 180° and 270°.

the rotation has order 4 and the CD diagram
has two point joined by a double line
or a line with index 4.
We could consider other angle. Two reflections at 36° give a five-fold rotation this would be shown as a triple line or a line with index 5. Two reflections at 30° give a six-fold rotation with a quadruple line joining the points in the CD diagram. For what follows we are less interested in these higher fold reflections.

| Description | Diagram | Notes |
| Single generator | ||
| Two generator of order 2 | For example two reflections at 90°. Doing the first reflection followed second gives the same as the second followed by the first, so these are said to commute, are draw with no single line joining them. | |
| Two generator of order 3 | e.g. two reflections 60°. Joined with a single line. | |
| Two generator of order 4 | e.g. two reflections at 45°. Joined with line with index 4. | |
| Two generator of order 5 | e.g. two reflections at 36°. Joined with line with index 5. | |
| Two generator of order 6 | e.g. two reflections at 30°. Joined with line with index 6. |
For other groups we need to consider the symmetry of objects in higher dimensions. To get to A3 we can consider the symmetries of the tetrahedron. There are six possible reflection, one for each edge, each reflection swaps two of the vertices. We just need three of these to generate the whole group. Here is a tetrahedron with those

3D Model
and just the reflections.

The arrangement of these reflections is
slightly odd. Two (red and green) are at right angles to each other
the other pairs (red-blue, green-blue) are at 60°. In the CD diagram there are
three nodes red, blue, green. As the red green reflection have order 2 they have no lines between them,
the red-blue and blue-green pairs are both of order 3 so have a single line joining them
We could generalize this in two ways: going up a dimension. The 4D
version of a simplex is the 5-cell with 5 points, 10 edges, 10 faces,
5 tetrahedra. This give the group A4 generated by four reflections, A,
B, C, D. A-B are at 60° as are B-C and C-D. The other pairs of
reflections A-C, A-D, B-D are at right angle so no line in the CD and
the full CD is:
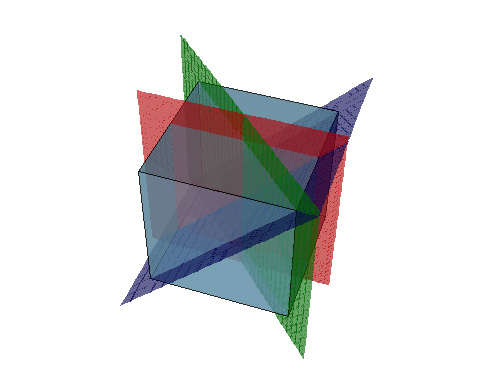
We could also consider other 3D polyhedra, the cube can be generated by three reflection.
3D Model
Red and Green are at 45° so have a double line in the CD Green and
Blue are at 60° so have a single line Blue and Red are at right angles
so have no line in the CD. The full CD is
To get to the interesting systems like D4, we need to consider 4D polytopes. The demi-tesseract has a D4 structure. This will have four reflection A B C D one of these B will at 60° to the other three reflections. The other combinations will be at right-angles.
To understand this group lets return to the symmetry of the tetrahedron. Take a tetrahedron centred at the origin with vertices $a=(1,-1,1), b=(-1,1,1), c=(1,1,-1), d=(-1,-1,-1)$. The three reflections used as generators are $$G=\begin{pmatrix}0 & 1 & 0\\ 1 & 0 & 0 \\ 0 & 0 & 1\end{pmatrix}, R=\begin{pmatrix}0 & -1 & 0\\ -1 & 0 & 0 \\ 0 & 0 & 1\end{pmatrix}, B=\begin{pmatrix}1 & 0 & 0\\ 0 & 0 & 1 \\ 0 & 1 & 0\end{pmatrix} $$ $G$ swaps the first two coordinates and sends $a\to b$, $b\to a$, $c\to c$, $d\to d$, $R$ swaps and negates the first two coordinates sends $a\to a$, $b\to b$, $c\to d$, $d\to c$, $B$ swaps the last two coordinates sends $a\to c$, $b\to b$, $c\to a$, $d\to d$. See full list of elements.
To go to four dimensions we have a Demitesseract with vertices of two copies of a tetrahedron $a=(1,-1,1,1), b=(-1,1,1,1), c=(1,1,-1,1), d=(-1,-1,-1,1)$, $a'=(-1,1,-1,-1), b'=(1,-1,-1,-1), c'=(-1,-1,1,-1), d'=(1,1,1,-1)$.
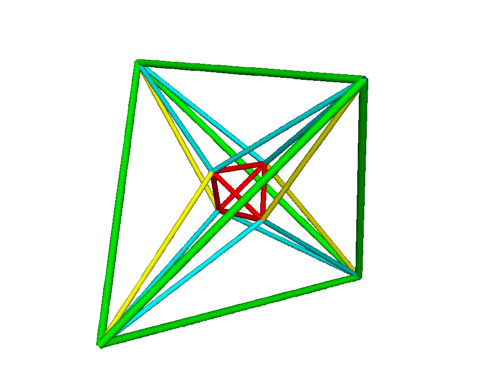
The generators are the same as for A3 which also leaves the last coordinate unchanged
$$ G=\begin{pmatrix}0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}, R=\begin{pmatrix}0 & -1 & 0 & 0\\ -1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}, B=\begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix} $$ plus a forth that swaps the last two coordinates $$ Y=\begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0\end{pmatrix}, $$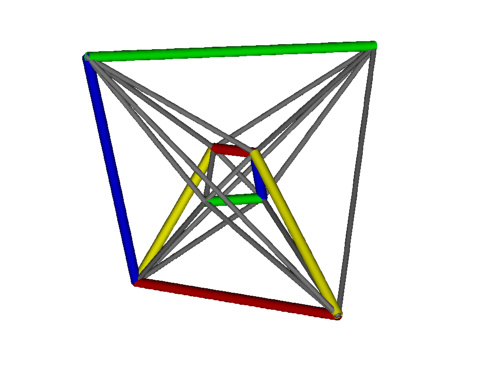
3D Model
Looking at the action of the generators on the vertices $G: a\leftrightarrow b, a'\leftrightarrow b'$, $R: c\leftrightarrow d, c'\leftrightarrow d'$, $B: a\leftrightarrow c, a'\leftrightarrow c'$, $Y: c\leftrightarrow d', d\leftrightarrow c'$.
Combining pair of generators we find $G R=R G$, $G Y=Y G$, $R Y=Y R$ so
each pair of these commute and are not linked in the CD diagram.
However $B R\neq R B, B G\neq G B, B Y\neq Y B$
and $(B R)^3=(B G)^3=(B Y)^3=I$ so these pairs have order 3 and are joined by a line in the
CD diagram.
Note how the blue edge is connected to edges of each other colour indicating a non trivial relationship.
Further elements are created by combining three of more of these elements,
so for example $G R B, G R Y, G B G, G B R,$ $G B Y, G Y B, R B G, R B R,$ $R B Y, R Y B,
B G R, B G Y,$ $B R Y, B Y B, Y B G, Y B R$ are all unique elements. In total
there are 192 unique elements, the most complex being $ G R B G R B Y B G R B Y$, which is an inversion.
See full list of elements.