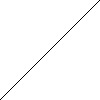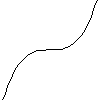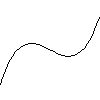Stable Maps and Unfoldings
Functions of one variable
Lets study the simplest case: Maps from $\mathbb R$ to $\mathbb R$.
Here we have a much simpler set of
singularities which just consist of the A-series:
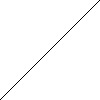 |
A0
|
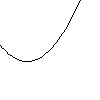
 |
A1
|
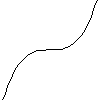 |
A2
|
 |
A3
|
We notice in this case how the type of singularity depends on how many
derivatives vanish. This is one of the roots of singularity theory, how
can you generalise the classification of functions interms of vanishing
defivatives to general maps from $\mathbb R^n$ to $\mathbb R^p$ ? As we have
seen in the previous section this is not entirly straight forward.
For example we
get the D and E series when we have two or more variables
this does not occur for functions of one variable.
Deforming the functions
Now what happens if we slightly perterb the function. If we
add an extra term term to the function, say replacing $x^3$ by $x^3 + a x$
we get two cases:
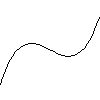 |
- $f(x) = x^3-\tfrac{1}{2} x$
|
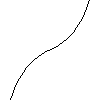 |
- $f(x) = x^3+\tfrac{1}{2} x$
|
In the first we have two A1 singularities the max and min but in the
second there are no singularities. We say that the A2 two point
is un-stable as it normally vanishes
when we disturb the function.
On the otherhand an A1 singularity is
stable as we can add a small multiple
of any function and we will still get and A2 singularity. For
example we could have
$x^2+a x$ or $x^2 + a x^3$ and for suficiently small values
of a there will be a point near the origin which is an A1
singularity.
Note in the second of these a second A1 point has appeared, this need
not concern us here as we are only interested in the local behaviour,
for very small values of a this other singularity will be a long
way from the origin.
Maps from $\mathbb R^2$ to $\mathbb R^2$
In the case of maps from $\mathbb R$ to $\mathbb R$ we only have one type
of stable singularity: A1, and for maps from $\mathbb R^3$ to $\mathbb R$
none of the singularities are stable (adding $a x$ to $x^2-y^2-z^2$ splits
the zero set into two smooth pieces). Things get more interesting
if we study maps from the plane to the plane. Here we have two cases
the
fold $(x,y)\to(x,y^2)$ and the
cusp $(x,y)\to(x,y^3)$.
To help visulise these maps
we can think of them as the composition of a map from $\mathbb R^2$ into
$\mathbb R^3$ (this gives a parametrisation of a surface in three space)
and projections into the plane.
For the fold map we parametrise the surface
by $(x,y)\to(x,y^2,y)$ and project into the plane using $(x,y,z)\to(x,y)$.
The composition gives $(x,y)\to(x,y^2)$. The picture below show the surface
and its projection, the projection direction is vertical, and the black
lines indicate the fold points.
 |
The Fold
- $(x,y)\to(x,y^2)$
- Composition of $(x,y)\to(x,y^2,y)$
- and $(x,y,z)\to(x,y)$
|
 |
The Cusp
- $(x,y)\to(x,y^3+x y)$
- Composition of $(x,y)\to(x,y^3+x y,y)$
- and $(x,y,z)\to(x,y)$
|
Maps from $\mathbb R^3$ to $\mathbb R^3$
Things get more interesting when we examine maps from
3-space to 3-space. We have the equivilent of folds and
cusps (for example $(x,y,z)\to(x,y,z^2)$ and
$(x,y,z)\to(x,y,z^3+y z)$) but we also get another stable map:
$(x,y,z)\to(x,y,z^4+x z + y z^2)$
called the
swallowtail map.
This time we will just draw the critical set, i.e. the
points in the source where the map is singular, and the
image of the critical set which is called the discriminant.
At a typical point on the critical set the map will be locally a
fold map, at some points (marked in black) the map is locally a cusp
map and the image of such points forms a cispidal edge,
and at the origin its of swallowtail type.
The Swallowtail
 |
Source
- Critical Set of the map $(x,y,z)\to(x,y,z^4+x z + y z^2)$
- i.e. $(x,y,z)$ such that $4 z^3 + x + 2 y z = 0$
|
 |
Target
- Discriminant of the map $(x,y,z)\to(x,y,z^4+x z + y z^2)$
- i.e. image of the critical set
|